What Is The Square Root Of 26
Juapaving
Mar 26, 2025 · 5 min read
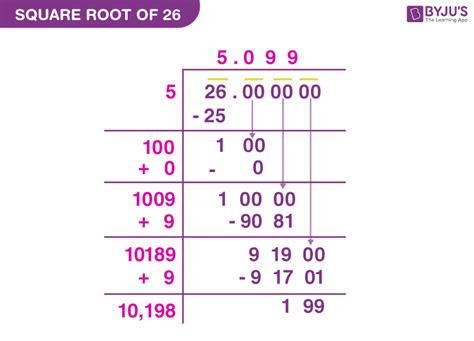
Table of Contents
What is the Square Root of 26? A Deep Dive into Irrational Numbers
The seemingly simple question, "What is the square root of 26?" opens a fascinating window into the world of mathematics, specifically the realm of irrational numbers. While a simple calculator will provide a decimal approximation, understanding the true nature of √26 requires a deeper exploration of its properties and significance. This article will delve into the calculation, the properties of irrational numbers, and the broader mathematical context of this seemingly straightforward question.
Understanding Square Roots
Before diving into the specifics of √26, let's establish a foundational understanding of square roots. The square root of a number (x) is a value (y) that, when multiplied by itself, equals x. In mathematical terms: y² = x, therefore y = √x. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9.
Calculating the Square Root of 26: An Approximation
Unlike the square root of a perfect square (like 9, 16, or 25), the square root of 26 is not a whole number. It's an irrational number, meaning it cannot be expressed as a simple fraction (a ratio of two integers). This means its decimal representation goes on forever without repeating.
Calculators provide an approximation of √26 as approximately 5.099. However, this is just a rounded-off value. The actual value extends infinitely. This infinite, non-repeating nature is a defining characteristic of irrational numbers.
Irrational Numbers: A Deeper Look
The discovery of irrational numbers was a significant milestone in the history of mathematics. It challenged the prevailing belief that all numbers could be expressed as ratios. The most famous example of an irrational number is π (pi), the ratio of a circle's circumference to its diameter. Other well-known irrational numbers include e (Euler's number), the golden ratio (φ), and, of course, the square root of most non-perfect squares, such as √26.
Properties of Irrational Numbers
- Non-terminating and non-repeating decimals: As mentioned earlier, the decimal representation of irrational numbers goes on forever without exhibiting a repeating pattern.
- Cannot be expressed as a fraction: They cannot be written as a ratio of two integers (a/b, where 'a' and 'b' are integers and b≠0).
- Dense on the number line: Between any two irrational numbers, no matter how close together, there are infinitely many other irrational numbers.
- Uncountable: While the set of rational numbers is countable (meaning they can be put into a one-to-one correspondence with the natural numbers), the set of irrational numbers is uncountable, indicating a much larger infinity.
Methods for Approximating √26
While we cannot find an exact value for √26, several methods can provide increasingly accurate approximations:
1. Using a Calculator:
The simplest method is using a calculator or computer software. These tools utilize sophisticated algorithms to calculate approximations to many decimal places. However, it's crucial to remember that this is still an approximation, not the exact value.
2. The Babylonian Method (or Heron's Method):
This iterative method refines an initial guess to progressively closer approximations. It involves the following steps:
- Make an initial guess: Let's start with 5, as 5² = 25, which is close to 26.
- Improve the guess: Divide 26 by the initial guess (26/5 = 5.2).
- Average: Average the initial guess and the result from step 2: (5 + 5.2)/2 = 5.1.
- Repeat: Use 5.1 as the new guess and repeat steps 2 and 3. This process is continued until the desired level of accuracy is achieved.
With each iteration, the approximation gets closer to the actual value of √26.
3. Taylor Series Expansion:
This advanced mathematical technique involves expressing the function as an infinite sum of terms. While complex, it provides a highly accurate approximation of √26 with more terms added to the series. This method is typically used in advanced mathematical contexts and requires a strong understanding of calculus.
4. Numerical Methods:
Various numerical methods, such as the Newton-Raphson method, can be employed to find increasingly accurate approximations of √26. These methods involve iterative processes and require a strong mathematical background.
The Significance of Irrational Numbers
The existence and importance of irrational numbers extend far beyond simple calculations like finding the square root of 26. They have profound implications across numerous areas of mathematics and science:
- Geometry: Irrational numbers are essential in geometric calculations, particularly those involving circles and other curved shapes. The circumference and area of a circle, for instance, involve π, an irrational number.
- Trigonometry: Trigonometric functions like sine, cosine, and tangent often involve irrational numbers.
- Calculus: Irrational numbers are frequently encountered in calculus, especially when dealing with limits, derivatives, and integrals.
- Physics: Many physical phenomena are described by equations involving irrational numbers. For example, the calculation of gravitational forces or the analysis of wave motion often involves irrational numbers.
√26 in Real-World Applications
While √26 might not seem immediately relevant to everyday life, it appears in various contexts:
- Engineering: In structural engineering, calculating diagonal lengths or distances often involves square roots, including cases where the result is an irrational number.
- Computer Graphics: Generating images and animations often involves calculations with square roots to determine positions and distances.
- Physics Simulations: Simulating physical systems often uses equations that include irrational numbers.
Conclusion
The seemingly simple question of "What is the square root of 26?" leads to a rich exploration of irrational numbers, their properties, and their wide-ranging applications across mathematics and science. While we can only approximate its value using various methods, the true nature of √26 as an irrational number, characterized by its infinite and non-repeating decimal representation, highlights a fundamental aspect of mathematics: the existence of numbers that defy simple, fractional representation. Understanding this concept is key to a deeper appreciation of the complexities and beauty of the mathematical world. The quest to understand and approximate √26, therefore, becomes a journey into the heart of mathematical reasoning and the elegance of irrational numbers.
Latest Posts
Latest Posts
-
Whats The Prime Factorization Of 15
Mar 29, 2025
-
37 Inches Is How Many Feet
Mar 29, 2025
-
Find The Lcm Of 3 And 5
Mar 29, 2025
-
How Do You Do Average In Math
Mar 29, 2025
-
Liquids At Room Temperature Periodic Table
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 26 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
