What's The Prime Factorization Of 15
Juapaving
Mar 29, 2025 · 5 min read
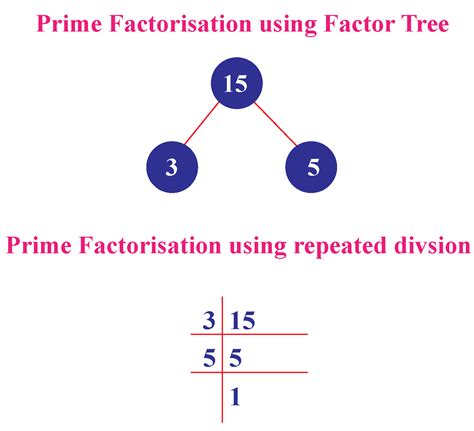
Table of Contents
What's the Prime Factorization of 15? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What's the prime factorization of 15?" opens a door to a fascinating world of number theory, fundamental to mathematics and computer science. While the answer itself is straightforward, exploring the concepts behind it reveals a wealth of mathematical beauty and practical applications. This article will not only answer the question but delve into the underlying principles of prime numbers, prime factorization, and their significance in various fields.
Understanding Prime Numbers
Before tackling the prime factorization of 15, we need a solid grasp of what prime numbers are. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This means it cannot be expressed as a product of two smaller natural numbers. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number.
Key Characteristics of Prime Numbers:
- Divisibility: Only divisible by 1 and itself.
- Infinitude: There are infinitely many prime numbers. This was famously proven by Euclid.
- Distribution: While their distribution appears somewhat random, there are patterns and conjectures related to their spacing and frequency. The Prime Number Theorem provides an approximation of the number of primes less than a given number.
- Fundamental Building Blocks: Prime numbers are the fundamental building blocks of all other natural numbers greater than 1. This is the essence of the Fundamental Theorem of Arithmetic.
The Fundamental Theorem of Arithmetic
The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This theorem is crucial because it establishes the uniqueness of prime factorization. No matter how you factor a number, you will always end up with the same set of prime factors. This uniqueness is fundamental to many mathematical proofs and algorithms.
Finding the Prime Factorization of 15
Now, let's finally address the question: what is the prime factorization of 15? To find the prime factorization, we systematically break down the number into its prime components.
- Start with the smallest prime number, 2: 15 is not divisible by 2 (it's an odd number).
- Move to the next prime number, 3: 15 is divisible by 3 (15 ÷ 3 = 5).
- The result is 5: 5 is itself a prime number.
Therefore, the prime factorization of 15 is 3 x 5. This means that 15 can be uniquely expressed as the product of the prime numbers 3 and 5.
Methods for Finding Prime Factorization
While the prime factorization of 15 was straightforward, larger numbers require more systematic approaches. Here are some common methods:
1. Factor Tree Method
This is a visual method where you repeatedly branch out factors until you reach only prime numbers.
15
/ \
3 5
In this tree, 15 is broken down into its factors 3 and 5, both of which are prime numbers. Thus, the prime factorization is 3 x 5.
2. Repeated Division Method
This method involves repeatedly dividing the number by the smallest prime number that divides it evenly, continuing until the quotient is 1.
- Divide 15 by 3: 15 ÷ 3 = 5
- Divide 5 by 5: 5 ÷ 5 = 1
The prime factors are 3 and 5.
Applications of Prime Factorization
Prime factorization might seem like an abstract mathematical concept, but it has surprising practical applications in various fields:
1. Cryptography
Prime factorization is the cornerstone of many modern cryptographic systems, such as RSA encryption. RSA relies on the difficulty of factoring very large numbers into their prime components. The security of these systems depends on the computational infeasibility of factoring extremely large semi-primes (numbers that are the product of two large prime numbers).
2. Computer Science
Prime factorization is used in various algorithms and data structures. For instance, it plays a role in efficient calculations, hashing functions, and certain types of data compression.
3. Number Theory
Prime factorization is fundamental to numerous branches of number theory, including the study of modular arithmetic, Diophantine equations, and the distribution of prime numbers.
4. Coding Theory
In coding theory, prime numbers are used in the design of error-correcting codes. These codes ensure reliable data transmission, especially crucial in applications like satellite communication and data storage.
5. Abstract Algebra
Prime numbers and prime factorization are vital in abstract algebra, particularly in the study of rings and fields, which are fundamental algebraic structures with wide-ranging applications in mathematics and other sciences.
Advanced Concepts Related to Prime Factorization
While we've covered the basics, the world of prime factorization extends far beyond the simple example of 15. Here are some more advanced concepts:
-
Greatest Common Divisor (GCD): Finding the GCD of two numbers involves identifying the largest number that divides both without leaving a remainder. Prime factorization greatly simplifies this process. By comparing the prime factorization of two numbers, you can easily identify their common prime factors and compute their GCD.
-
Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of both numbers. Again, prime factorization simplifies the calculation of the LCM.
-
Modular Arithmetic: Prime numbers are crucial in modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus). Modular arithmetic is essential in cryptography and computer science.
-
Prime Number Theorem: This theorem provides an approximation of the density of prime numbers. It states that the number of primes less than a given number x is approximately x/ln(x), where ln(x) is the natural logarithm of x.
-
Riemann Hypothesis: One of the most famous unsolved problems in mathematics, the Riemann Hypothesis is related to the distribution of prime numbers and has profound implications for number theory.
Conclusion: The Enduring Importance of Prime Factorization
The prime factorization of 15, while simple in its answer (3 x 5), serves as a gateway to a deep and rich area of mathematics. Understanding prime numbers and prime factorization is essential not just for mathematical study but also for appreciating their significant role in cryptography, computer science, and other fields. The seemingly simple question about the prime factorization of 15 reveals a profound truth: these fundamental building blocks of numbers underpin many of the technologies and mathematical structures that shape our world. The exploration of prime numbers is an ongoing journey, with many mysteries still waiting to be unraveled.
Latest Posts
Latest Posts
-
Ionic Compounds Are Composed Of What Particles
Apr 01, 2025
-
What Is 3 33333 As A Fraction
Apr 01, 2025
-
What Does A Prokaryotic Cell Not Have
Apr 01, 2025
-
What Are More Things About The Major Components Of Soil
Apr 01, 2025
-
What Is The Lcm Of 5 6 7
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What's The Prime Factorization Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
