Find The Lcm Of 3 And 5
Juapaving
Mar 29, 2025 · 5 min read
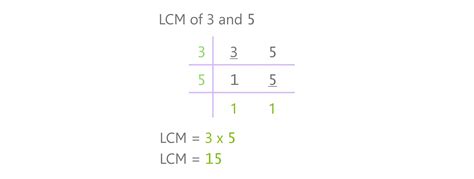
Table of Contents
Finding the LCM of 3 and 5: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in arithmetic with wide-ranging applications in various fields, from scheduling tasks to simplifying fractions. This article provides a comprehensive guide to finding the LCM of 3 and 5, exploring multiple methods and delving into the underlying mathematical principles. We'll also touch upon the broader context of LCM calculations and their significance.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's clarify what the least common multiple (LCM) actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. For instance, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The common multiples of 2 and 3 are 6, 12, 18, 24, 30, and so on. The smallest of these common multiples is 6, therefore, the LCM(2, 3) = 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 3 and 5. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50...
By comparing the two lists, we observe that the smallest common multiple is 15. Therefore, the LCM(3, 5) = 15.
This method is simple and intuitive, but it can become cumbersome and time-consuming when dealing with larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 5: 5 (5 is a prime number)
The prime factorization method relies on the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
Once we have the prime factorizations, we identify the highest power of each prime factor present in either factorization. In this case:
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
To find the LCM, we multiply these highest powers together: 3 x 5 = 15. Therefore, LCM(3, 5) = 15.
This method is more systematic and efficient than listing multiples, particularly when dealing with larger numbers or multiple numbers.
Method 3: Using the Formula (For Two Numbers)
For two numbers, a and b, there's a handy formula that utilizes the greatest common divisor (GCD):
LCM(a, b) = (|a * b|) / GCD(a, b)
Where |a * b| represents the absolute value of the product of a and b.
First, we need to find the GCD of 3 and 5. Since 3 and 5 are both prime numbers and have no common factors other than 1, their GCD is 1.
Now, we apply the formula:
LCM(3, 5) = (|3 * 5|) / GCD(3, 5) = 15 / 1 = 15
This formula provides a concise and efficient way to calculate the LCM, especially when the GCD is easily determined.
Understanding the Relationship Between LCM and GCD
The LCM and GCD are intrinsically linked. For any two integers a and b, the product of their LCM and GCD is always equal to the product of the two numbers:
LCM(a, b) * GCD(a, b) = a * b
This relationship is a powerful tool for calculating either the LCM or GCD if the other is known. In our example:
LCM(3, 5) * GCD(3, 5) = 15 * 1 = 15 = 3 * 5
This confirms the accuracy of our LCM calculation.
Applications of LCM
The concept of LCM finds numerous applications in various fields:
-
Scheduling: Imagine two buses arrive at a bus stop at intervals of 3 minutes and 5 minutes respectively. The LCM(3, 5) = 15 minutes determines when both buses will arrive at the stop simultaneously.
-
Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions. This ensures we find a common denominator for simplifying the calculation.
-
Modular Arithmetic: LCM plays a vital role in solving problems involving congruences and modular arithmetic, which are fundamental concepts in number theory and cryptography.
-
Cyclic Processes: LCM is used to determine when repeating events will coincide, like the cycles of planets or machinery.
-
Music Theory: LCM is employed in music theory to determine the least common multiple of the durations of different musical notes.
-
Project Management: In project scheduling, LCM helps in finding the shortest time for completing tasks with different durations.
Beyond Two Numbers: Finding LCM of Multiple Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method remains particularly useful. For instance, let's find the LCM of 3, 5, and 6:
-
Prime factorization:
- 3 = 3
- 5 = 5
- 6 = 2 x 3
-
Identify highest powers:
- 2¹ = 2
- 3¹ = 3
- 5¹ = 5
-
Multiply highest powers: 2 x 3 x 5 = 30
Therefore, LCM(3, 5, 6) = 30.
The listing multiples method becomes increasingly cumbersome with more numbers, making prime factorization a more efficient and reliable approach.
Conclusion: Mastering LCM Calculations
Finding the least common multiple is a fundamental skill with wide-ranging applications. While the simple listing method works for small numbers, the prime factorization method provides a more robust and efficient approach, especially when dealing with larger numbers or multiple numbers. Understanding the relationship between LCM and GCD further enhances problem-solving capabilities. Mastering LCM calculations is an essential step towards a deeper understanding of number theory and its practical applications in various fields. By understanding these methods and their underlying principles, you'll be well-equipped to tackle LCM problems with confidence and efficiency. Remember to practice regularly to reinforce your understanding and improve your speed and accuracy.
Latest Posts
Latest Posts
-
What Does A Prokaryotic Cell Not Have
Apr 01, 2025
-
What Are More Things About The Major Components Of Soil
Apr 01, 2025
-
What Is The Lcm Of 5 6 7
Apr 01, 2025
-
Find The Complementary And Supplementary Angles
Apr 01, 2025
-
What Is The Specific Heat Of Liquid Water
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Find The Lcm Of 3 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
