How Do You Do Average In Math
Juapaving
Mar 29, 2025 · 5 min read
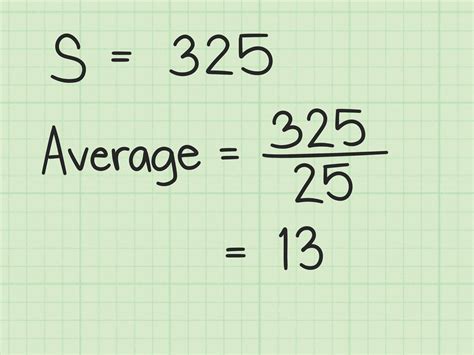
Table of Contents
How to Ace Your Math Average: A Comprehensive Guide
Math can be a challenging subject for many, but mastering the art of calculating averages is a fundamental skill with wide-ranging applications. Whether you're a student aiming for top grades, a professional analyzing data, or simply someone curious about statistics, understanding how to calculate averages is crucial. This comprehensive guide delves into various types of averages, provides step-by-step instructions, explores real-world applications, and offers practical tips to enhance your understanding and improve your math skills.
Understanding Different Types of Averages
Before diving into calculations, let's clarify the different types of averages:
1. Mean: The Most Common Average
The mean, often referred to as the average, is the sum of all numbers divided by the total count of numbers. This is the most commonly used type of average.
Formula: Mean = (Sum of all numbers) / (Total number of values)
Example: Find the mean of 5, 10, 15, and 20.
- Sum: 5 + 10 + 15 + 20 = 50
- Total Count: 4
- Mean: 50 / 4 = 12.5
2. Median: The Middle Value
The median is the middle value in a dataset when the numbers are arranged in ascending order. If there's an even number of values, the median is the average of the two middle numbers. The median is less sensitive to outliers (extremely high or low values) than the mean.
Example: Find the median of 2, 5, 8, 11, 15.
The middle value is 8.
Example with Even Numbers: Find the median of 2, 5, 8, 11.
The two middle values are 5 and 8. The median is (5 + 8) / 2 = 6.5
3. Mode: The Most Frequent Value
The mode is the value that appears most frequently in a dataset. A dataset can have one mode, more than one mode (multimodal), or no mode at all.
Example: Find the mode of 2, 4, 4, 5, 6, 6, 6, 7.
The mode is 6, as it appears most frequently.
4. Range: Spread of the Data
While not strictly an average, the range provides valuable information about the spread of data. It's the difference between the highest and lowest values in a dataset.
Formula: Range = Highest Value - Lowest Value
Example: Find the range of 2, 5, 8, 11, 15.
Range = 15 - 2 = 13
Step-by-Step Guide to Calculating Averages
Here's a detailed step-by-step guide to calculating each type of average:
Calculating the Mean:
- List the Numbers: Write down all the numbers in your dataset.
- Add the Numbers: Sum up all the numbers.
- Count the Numbers: Determine the total number of values in your dataset.
- Divide: Divide the sum of the numbers by the total count. The result is the mean.
Calculating the Median:
- Order the Numbers: Arrange the numbers in ascending order (from smallest to largest).
- Find the Middle: If you have an odd number of values, the median is the middle value. If you have an even number of values, the median is the average of the two middle values.
Calculating the Mode:
- Count Occurrences: Count how many times each value appears in the dataset.
- Identify the Most Frequent: The value that appears most often is the mode. If multiple values appear with the same highest frequency, the dataset is multimodal.
Real-World Applications of Averages
Averages are used extensively in various fields:
- Business and Finance: Calculating average sales, profits, expenses, and customer satisfaction scores.
- Science: Analyzing experimental data, determining average temperatures, and calculating statistical significance.
- Education: Determining average grades, class performance, and student progress.
- Sports: Calculating average scores, batting averages, and team statistics.
- Healthcare: Tracking average patient recovery times, blood pressure, and other vital signs.
Tips for Improving Your Math Skills and Average Calculations
- Practice Regularly: Consistent practice is key to mastering any math skill. Work through numerous examples and practice problems.
- Understand the Concepts: Don't just memorize formulas; understand the underlying concepts behind each calculation.
- Use Technology: Utilize calculators and software to aid your calculations, especially for large datasets. However, always try to understand the process manually first.
- Break Down Complex Problems: Divide complex problems into smaller, manageable steps.
- Seek Help When Needed: Don't hesitate to ask for help from teachers, tutors, or classmates if you're struggling.
- Visual Aids: Graphs and charts can help visualize data and make understanding averages easier.
- Real-World Connections: Relate the concepts to real-world scenarios to improve understanding and retention. For example, relate calculating average scores to calculating your average grade in a class.
- Focus on Accuracy: Double-check your work to minimize errors, especially in the addition and division steps.
Advanced Concepts and Considerations
-
Weighted Average: In some cases, certain values contribute more significantly to the overall average. A weighted average assigns different weights to different values, reflecting their relative importance. For example, in a course with different weighted assignments (e.g., homework 20%, quizzes 30%, exams 50%), a weighted average is used to calculate the final grade.
-
Geometric Mean: Used for data that involves multiplicative relationships. The geometric mean is calculated by multiplying all the numbers and then taking the nth root, where n is the number of values. This is particularly useful for calculating average growth rates or returns over time.
-
Harmonic Mean: Appropriate for data representing rates or ratios. The harmonic mean is the reciprocal of the arithmetic mean of the reciprocals of the data values. This is often used in situations involving averages of speeds or rates.
Conclusion: Mastering the Art of Averages
Calculating averages is a fundamental skill with broad applications. By understanding the different types of averages, mastering the calculation steps, and practicing regularly, you can significantly enhance your math skills and confidently apply this knowledge to various real-world situations. Remember, practice makes perfect! The more you work with averages, the more comfortable and proficient you'll become. Don't be afraid to explore advanced concepts and challenge yourself with complex problems. With dedication and the right approach, you can truly master the art of averaging.
Latest Posts
Latest Posts
-
What Is 3 33333 As A Fraction
Apr 01, 2025
-
What Does A Prokaryotic Cell Not Have
Apr 01, 2025
-
What Are More Things About The Major Components Of Soil
Apr 01, 2025
-
What Is The Lcm Of 5 6 7
Apr 01, 2025
-
Find The Complementary And Supplementary Angles
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Do You Do Average In Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
