What Is The Percentage Of 3/7
Juapaving
Mar 21, 2025 · 5 min read
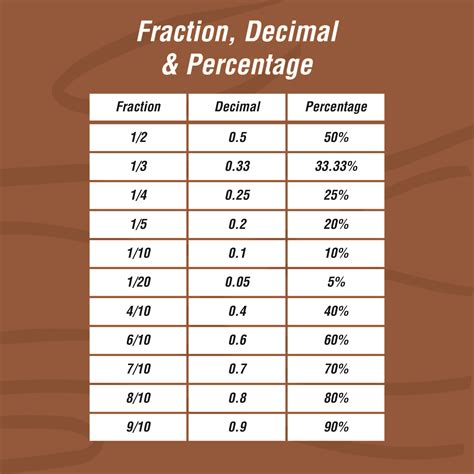
Table of Contents
What is the Percentage of 3/7? A Deep Dive into Fractions and Percentages
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding financial statements and statistical data. This article delves deep into the process of converting the fraction 3/7 into a percentage, exploring the underlying concepts, different calculation methods, and practical applications.
Understanding Fractions and Percentages
Before we jump into calculating the percentage of 3/7, let's solidify our understanding of the core concepts.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we're considering, while the denominator represents the total number of equal parts the whole is divided into. For example, in the fraction 3/7, 3 is the numerator and 7 is the denominator. This means we are considering 3 parts out of a total of 7 equal parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. It represents a proportion out of a total of 100 parts. The symbol "%" is used to denote a percentage. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
Calculating the Percentage of 3/7: Method 1 - Direct Conversion
The most straightforward method to convert a fraction to a percentage involves two steps:
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (7). 3 ÷ 7 ≈ 0.42857142857
-
Multiply the decimal by 100: This will give you the percentage. 0.42857142857 × 100 ≈ 42.857%
Therefore, 3/7 is approximately 42.86%. Note that we often round percentages to two decimal places for practicality.
Understanding the Approximation
It's crucial to understand that the percentage we calculated is an approximation. The decimal representation of 3/7 is a non-terminating decimal (it goes on forever without repeating in a short pattern). Therefore, any percentage we calculate will be a rounded approximation. The level of precision depends on how many decimal places we use in our calculations.
Calculating the Percentage of 3/7: Method 2 - Using Proportions
Another approach involves setting up a proportion:
We know that a percentage is a fraction out of 100. We can set up the following proportion:
3/7 = x/100
To solve for x (the percentage), we cross-multiply:
7x = 300
x = 300/7
x ≈ 42.857
Therefore, x ≈ 42.86%, confirming our previous result. This method reinforces the understanding that percentage is simply a different way of expressing a fraction with a denominator of 100.
Practical Applications of Converting 3/7 to a Percentage
Understanding how to convert fractions like 3/7 to percentages is essential in various real-world scenarios:
1. Sales and Discounts: Imagine a store offering a discount of 3/7 on all items. Knowing that this is approximately a 42.86% discount allows customers to easily understand the savings.
2. Financial Calculations: In finance, fractions and percentages are used extensively. For example, calculating interest rates, profit margins, or understanding investment returns often involves working with fractions and converting them to percentages for better interpretation.
3. Statistics and Probability: Statistical analysis and probability calculations frequently involve fractions. Converting these fractions to percentages makes it easier to understand and communicate the results. For example, if the probability of an event occurring is 3/7, then this is approximately a 42.86% chance of the event happening.
4. Everyday Calculations: Even simple tasks like splitting a bill among friends or calculating the proportion of ingredients in a recipe may involve fractions, which are often easier to grasp when converted into percentages.
Beyond the Basics: Working with More Complex Fractions
While 3/7 is a relatively simple fraction, the same principles apply to more complex fractions. The methods described above—direct conversion and proportions—can be used to convert any fraction into a percentage.
For instance, consider the fraction 15/23. Using the direct conversion method:
- 15 ÷ 23 ≈ 0.65217
- 0.65217 × 100 ≈ 65.22%
Therefore, 15/23 is approximately 65.22%.
The key takeaway is that understanding the fundamental relationship between fractions and percentages is essential for tackling various mathematical problems and for making sense of numerical information in everyday situations.
Expanding on the Concepts: Further Exploration
This article has focused on the practical methods of converting 3/7 into a percentage. However, the underlying mathematical concepts extend beyond this specific example. A deeper exploration might involve:
- Recurring Decimals: Understanding why the decimal representation of 3/7 is a recurring decimal and the implications for calculating its exact percentage.
- Significant Figures and Rounding: Analyzing the effect of the number of significant figures used in the calculations on the accuracy of the resulting percentage.
- Error Analysis: Investigating the potential for errors in the conversion process and methods to minimize them.
- Advanced Percentage Calculations: Exploring more complex percentage calculations, such as calculating percentage increases, decreases, or compound interest.
By delving deeper into these areas, you can build a more comprehensive understanding of fractions, percentages, and their applications in various fields. Mastering these fundamental mathematical skills is crucial for success in numerous academic and professional settings. This detailed exploration of the seemingly simple task of converting 3/7 to a percentage highlights the importance of understanding the underlying mathematical principles and their practical significance. It's more than just a calculation; it's a foundation for more advanced mathematical concepts and real-world applications.
Latest Posts
Latest Posts
-
Tap Water Mixture Or Pure Substance
Mar 28, 2025
-
The Role Of The Light Harvesting Complex Is To
Mar 28, 2025
-
Electrical Conductivity Physical Or Chemical Property
Mar 28, 2025
-
Why Do Atoms Want 8 Valence Electrons
Mar 28, 2025
-
Two Angles Whose Measures Have A Sum Of 180 Degrees
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 3/7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
