Two Angles Whose Measures Have A Sum Of 180 Degrees
Juapaving
Mar 28, 2025 · 5 min read
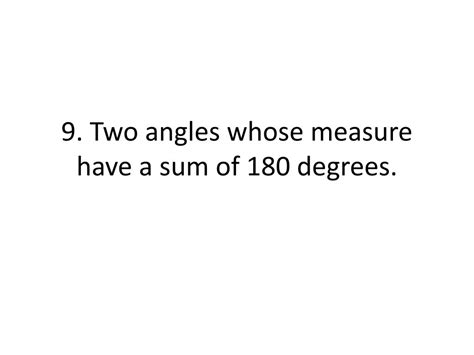
Table of Contents
Two Angles Whose Measures Have a Sum of 180 Degrees: A Deep Dive into Supplementary Angles
Understanding angles is fundamental to geometry and trigonometry. Among the various relationships between angles, the concept of supplementary angles holds significant importance. This comprehensive article will explore supplementary angles in detail, covering their definition, properties, applications, and how they relate to other angle types. We'll delve into practical examples and problem-solving techniques to solidify your grasp of this crucial geometric concept.
Defining Supplementary Angles
Two angles are considered supplementary if the sum of their measures equals 180 degrees. This is a crucial definition to remember. It's not simply about two angles being adjacent; they can be anywhere in space, as long as their combined measure adds up to 180°. For example, a 120° angle and a 60° angle are supplementary, regardless of their spatial arrangement.
Key Characteristics:
- Sum: The defining feature is the sum of 180°.
- Spatial Arrangement: Supplementary angles can be adjacent (sharing a common vertex and side) or non-adjacent (not sharing a common vertex or side).
- Types of Angles: Supplementary angles can be a combination of different angle types, including acute, obtuse, and right angles.
Supplementary Angles vs. Other Angle Relationships
It's important to distinguish supplementary angles from other angle relationships to avoid confusion. Here's a quick comparison:
Supplementary Angles vs. Complementary Angles
While supplementary angles add up to 180°, complementary angles add up to 90°. This is a significant difference. A 30° angle and a 60° angle are complementary, while a 30° angle and a 150° angle are supplementary.
Supplementary Angles vs. Adjacent Angles
Adjacent angles share a common vertex and side. While adjacent angles can be supplementary, they don't have to be. Two adjacent angles could add up to any value between 0° and 360°. Supplementary angles, however, are always defined by their 180° sum.
Supplementary Angles vs. Vertical Angles
Vertical angles are formed by intersecting lines and are always equal in measure. Vertical angles are not inherently related to the concept of supplementary angles, though they could be supplementary in certain configurations.
Identifying Supplementary Angles
Identifying supplementary angles involves analyzing the measures of angles. If the sum of the measures is 180 degrees, then you have supplementary angles. Let's consider a few examples:
Example 1: Adjacent Supplementary Angles
Imagine a straight line intersected by another line. The angles on one side of the intersecting line are adjacent and supplementary. If one angle measures 115°, the other angle must measure 180° - 115° = 65°.
Example 2: Non-Adjacent Supplementary Angles
Consider two angles, one measuring 130° and the other measuring 50°. These angles are supplementary because 130° + 50° = 180°, even though they are not adjacent.
Example 3: Finding a Supplementary Angle
If one angle measures x degrees and its supplementary angle measures y degrees, we can express their relationship as: x + y = 180°. To find the measure of one angle, given the measure of the other, simply solve the equation for the unknown variable.
Applications of Supplementary Angles
Supplementary angles have widespread applications across various fields, including:
Geometry and Trigonometry
Supplementary angles are fundamental to solving geometric problems involving triangles, quadrilaterals, and other polygons. Understanding supplementary angles allows us to calculate unknown angles within these shapes. In trigonometry, supplementary angles play a key role in understanding trigonometric identities and solving trigonometric equations.
Engineering and Architecture
Engineers and architects use the concept of supplementary angles for designing structures, calculating angles in structural elements, and ensuring stability and balance. Precise angle calculations, including the use of supplementary angles, are essential for constructing stable and functional buildings and bridges.
Computer Graphics and Game Development
In computer graphics and game development, supplementary angles are used for manipulating objects, creating realistic perspectives, and rendering accurate images. The use of supplementary angles is essential for developing realistic simulations and interactive environments.
Navigation and Surveying
Supplementary angles have applications in navigation and surveying, used in determining directions, calculating distances, and accurately mapping terrain.
Solving Problems with Supplementary Angles
Let's look at some problems involving supplementary angles to illustrate how to apply this concept:
Problem 1: Two angles are supplementary. One angle measures 75°. What is the measure of the other angle?
Solution: Let the other angle be x. Since they are supplementary, their sum is 180°. Therefore, 75° + x = 180°. Solving for x, we get x = 180° - 75° = 105°.
Problem 2: Three angles, x, y, and z, are supplementary. x measures 40°, and y measures twice the measure of x. What is the measure of z?
Solution: Since y measures twice x, y = 2 * 40° = 80°. The sum of x, y, and z is 180°. Therefore, 40° + 80° + z = 180°. Solving for z, we find z = 180° - 40° - 80° = 60°.
Problem 3: An angle is supplementary to an angle that measures 110°. What kind of angle is the supplementary angle? (Acute, obtuse, right)
Solution: The supplementary angle measures 180° - 110° = 70°. Since 70° is less than 90°, the supplementary angle is an acute angle.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding, consider exploring these advanced topics related to supplementary angles:
- Supplementary Angles and Parallel Lines: Investigate how supplementary angles are related to the angles formed by a transversal intersecting parallel lines.
- Supplementary Angles in Polygons: Explore how supplementary angles are used to find the measures of interior and exterior angles of polygons.
- Supplementary Angles in Trigonometry: Delve into the trigonometric identities and equations that utilize supplementary angles.
- Linear Pairs: Understanding linear pairs, which are adjacent angles that form a straight line and are always supplementary, offers additional insight.
By mastering the concept of supplementary angles, you'll gain a strong foundation in geometry and its applications across various fields. Remember, the key is the 180° sum—a simple yet powerful concept that unlocks a deeper understanding of angles and their relationships. Practice solving different problems to solidify your understanding and become proficient in applying this fundamental geometric concept.
Latest Posts
Latest Posts
-
How Is A Square Similar To A Rhombus
Mar 31, 2025
-
Work Done For The Process Shown In The Figure Is
Mar 31, 2025
-
Write The Electron Configuration For A Neutral Atom Of Germanium
Mar 31, 2025
-
What Two Numbers Multiply To 32
Mar 31, 2025
-
Do Isotopes Have The Same Mass Number
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Two Angles Whose Measures Have A Sum Of 180 Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
