What Is The Lcm Of 2 And 3
Juapaving
Mar 26, 2025 · 6 min read
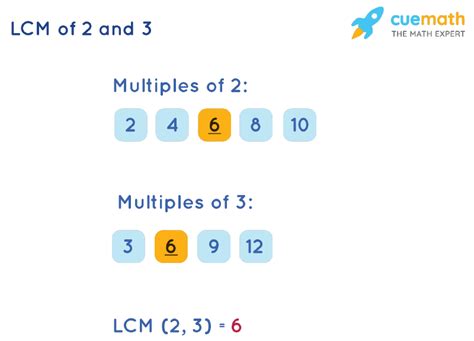
Table of Contents
What is the LCM of 2 and 3? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in arithmetic and number theory. It's a skill crucial for various applications, from simplifying fractions to solving complex algebraic equations. This article will comprehensively explore the question, "What is the LCM of 2 and 3?", while delving into the broader concept of LCMs, their calculation methods, and real-world applications.
Understanding Least Common Multiples (LCMs)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, the LCM of 4 and 6 is 12 because 12 is the smallest number that is divisible by both 4 and 6.
This concept is distinct from the greatest common divisor (GCD), which is the largest positive integer that divides each of the integers without leaving a remainder. While related, LCM and GCD are inverse concepts; understanding one helps grasp the other.
Why are LCMs Important?
LCMs have numerous practical applications in various fields:
- Fraction Arithmetic: Adding or subtracting fractions with different denominators requires finding the LCM of the denominators to obtain a common denominator. This simplifies the calculation process.
- Scheduling Problems: Determining when events with different periodicities will coincide requires finding the LCM of their periods. For example, if two machines operate with cycles of 2 and 3 hours respectively, the LCM helps find when they will both be at the starting point of their cycles simultaneously.
- Modular Arithmetic: LCMs are essential in solving problems related to modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus).
- Music Theory: The LCM is used in music to calculate the least common multiple of the note durations in a musical piece, useful for synchronization and rhythmic analysis.
- Computer Science: In programming and algorithm design, LCMs play a role in various optimization problems, particularly those involving timing and synchronization.
Calculating the LCM of 2 and 3
Now, let's address the core question: what is the LCM of 2 and 3?
We can use several methods to calculate the LCM of 2 and 3:
Method 1: Listing Multiples
The simplest method is to list the multiples of each number until we find the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16...
- Multiples of 3: 3, 6, 9, 12, 15, 18...
Notice that the smallest number appearing in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 2: Prime Factorization
This method is more efficient for larger numbers. First, find the prime factorization of each number.
- Prime factorization of 2: 2
- Prime factorization of 3: 3
Then, identify the highest power of each prime factor present in the factorizations. In this case, we have 2¹ and 3¹.
The LCM is the product of these highest powers: 2¹ * 3¹ = 6.
Method 3: Formula using GCD
There's a relationship between the LCM and GCD of two numbers (a and b):
LCM(a, b) * GCD(a, b) = a * b
The GCD of 2 and 3 is 1 (as 1 is the only common divisor). Therefore:
LCM(2, 3) * 1 = 2 * 3 LCM(2, 3) = 6
This formula provides a more elegant and efficient way to calculate the LCM, especially when dealing with larger numbers where finding the GCD is easier than listing multiples or directly finding the prime factorizations.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For example, let's find the LCM of 2, 3, and 4.
Method 1 (Listing Multiples):
This method becomes less practical with more numbers. You would need to list multiples of each number until you find the smallest common multiple.
Method 2 (Prime Factorization):
This is a more efficient approach.
- Prime factorization of 2: 2
- Prime factorization of 3: 3
- Prime factorization of 4: 2²
The highest powers of the prime factors are 2² and 3¹. Therefore, the LCM(2, 3, 4) = 2² * 3 = 12.
Method 3 (Formula using GCD - not directly applicable):
The formula LCM(a, b) * GCD(a, b) = a * b doesn't directly extend to more than two numbers. However, you can iteratively apply it. First find LCM(2,3) = 6 and then find LCM(6,4) = 12.
Real-World Applications of LCMs: Illustrative Examples
Let's explore some real-world scenarios where understanding LCMs is crucial:
1. Scheduling Train Departures: Two trains depart from the same station, one every 2 hours and the other every 3 hours. When will they depart simultaneously again?
The LCM of 2 and 3 is 6. The trains will depart simultaneously again after 6 hours.
2. Baking: A recipe calls for eggs to be added every 2 minutes and flour every 3 minutes. When will both ingredients be added at the same time?
The LCM of 2 and 3 is 6. Both ingredients will be added simultaneously after 6 minutes.
3. Concert Lighting: Two sets of lights flash, one every 2 seconds and the other every 3 seconds. When will both lights flash together?
The LCM of 2 and 3 is 6. Both lights will flash together every 6 seconds.
4. Synchronization in a Factory: Two machines in a factory complete their cycles every 2 minutes and 3 minutes respectively. When will they both be at the starting point of their cycles at the same time?
The LCM of 2 and 3 is 6. They will both be at the starting point simultaneously every 6 minutes.
5. Tile Laying: You want to lay tiles that are 2 cm and 3 cm wide. What's the smallest width you can cover with both tiles without any gaps or overlaps?
The LCM of 2 and 3 is 6. The smallest width you can cover is 6 cm.
Conclusion: The Significance of LCMs in Mathematics and Beyond
This in-depth exploration clarifies that the LCM of 2 and 3 is 6. However, the article extends far beyond this simple calculation. We've examined the fundamental definition of LCMs, explored different methods for calculating them, and demonstrated their broad applicability in diverse real-world scenarios. Understanding LCMs is not just a mathematical exercise; it's a valuable tool applicable across numerous fields, from scheduling and engineering to music and computer science. Mastering this concept provides a strong foundation for tackling more complex mathematical problems and enhances problem-solving skills in various contexts. The ability to efficiently calculate LCMs, particularly using prime factorization and understanding the relationship with GCD, is a skill with practical value in both academic and professional settings.
Latest Posts
Latest Posts
-
What The Square Root Of 24
Mar 28, 2025
-
What Is A Solution And A Mixture
Mar 28, 2025
-
What Is The Electron Configuration For Rb
Mar 28, 2025
-
What Is 25 Percent Of 150
Mar 28, 2025
-
Which Of The Following Energy Sources Drives The Hydrologic Cycle
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 2 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
