What The Square Root Of 24
Juapaving
Mar 28, 2025 · 6 min read
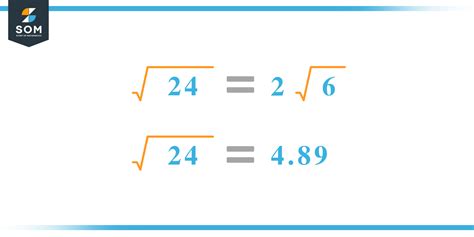
Table of Contents
What is the Square Root of 24? A Deep Dive into Irrational Numbers
The square root of 24, denoted as √24, is a fascinating mathematical concept that delves into the realm of irrational numbers. While it doesn't yield a neat whole number answer, understanding its properties and how to work with it is crucial for various mathematical applications. This comprehensive guide will explore the square root of 24, its calculation, simplification, its applications, and its place within the broader context of number theory.
Understanding Square Roots
Before diving into the specifics of √24, let's establish a fundamental understanding of square roots. A square root of a number is a value that, when multiplied by itself, equals the original number. For instance, the square root of 9 (√9) is 3 because 3 x 3 = 9. However, not all numbers have whole number square roots. This is where irrational numbers come into play.
Irrational Numbers: The Nature of √24
The square root of 24 is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation is non-terminating and non-repeating, meaning it goes on forever without ever settling into a predictable pattern. This is a key characteristic that distinguishes it from rational numbers like 1/2 or 0.75.
Calculating √24: Methods and Approximations
While we can't express √24 as a simple fraction, we can approximate its value using various methods.
1. Prime Factorization and Simplification
The most common approach involves prime factorization. We break down 24 into its prime factors:
24 = 2 x 2 x 2 x 3 = 2² x 6
This allows us to simplify the square root:
√24 = √(2² x 6) = √2² x √6 = 2√6
This simplified form, 2√6, is often preferred as it's more concise and easier to work with in mathematical calculations. It expresses the square root in terms of a rational number (2) and a simplified irrational number (√6).
2. Using a Calculator
A calculator provides a decimal approximation. The value of √24 is approximately 4.89897948557. However, keep in mind that this is only an approximation; the actual value extends infinitely.
3. Numerical Methods (for advanced understanding)
For those interested in a deeper mathematical dive, numerical methods like the Babylonian method (also known as Heron's method) can be used to iteratively approximate the square root to a desired level of accuracy. This method involves repeatedly refining an initial guess based on a specific formula.
Applications of √24
The square root of 24, or its simplified form 2√6, finds applications in various mathematical and real-world contexts.
1. Geometry
Imagine a right-angled triangle with legs of length 'a' and 'b', and a hypotenuse of length 'c'. The Pythagorean theorem states that a² + b² = c². If we know two sides of a right-angled triangle, we can use the square root to find the length of the third side. For example, if a = 2 and b = 4, then c = √(2² + 4²) = √20 = 2√5. While this isn't directly √24, the principle remains the same for other triangle dimensions where √24 might be the solution.
2. Physics and Engineering
Square roots frequently appear in physics and engineering formulas, such as calculations involving velocity, acceleration, and energy. These formulas often involve quadratic equations, the solutions to which often involve square roots. For instance, in calculating the velocity of an object under gravity, you might encounter expressions that need to be solved using square roots.
3. Computer Graphics and Game Development
In computer graphics and game development, calculating distances and positions of objects on a screen uses the Pythagorean theorem (and hence, square roots) extensively. The accurate representation of objects and their movements in virtual environments necessitates precise calculations, including those involving irrational numbers.
4. Statistics and Probability
The square root also plays a crucial role in statistics. For instance, the standard deviation, a measure of data dispersion, involves the square root of the variance.
Understanding the Relationship between √24 and Other Square Roots
The simplification of √24 to 2√6 highlights a valuable mathematical principle: we can often simplify square roots by factoring out perfect squares. This allows for a more manageable and understandable representation of the irrational number. This concept extends to other square roots as well. Understanding how to simplify these expressions is essential in various mathematical operations.
Furthermore, understanding the relationship between √24 and other square roots helps to conceptualize its value. For example, comparing it to √25 (which equals 5) gives a rough estimation of its magnitude. Since 24 is close to 25, √24 is slightly less than 5.
Approximating √24 without a Calculator
While calculators readily provide an approximation, understanding how to approximate √24 manually is a valuable skill that deepens our understanding of the number. One method involves using the concept of perfect squares. Since 4² = 16 and 5² = 25, we know √24 lies between 4 and 5. We can refine this approximation by considering that 24 is closer to 25 than to 16, suggesting that √24 is closer to 5 than to 4. More sophisticated methods, such as the Babylonian method, offer a way to iteratively refine this approximation to a desired level of accuracy.
Beyond the Calculation: Exploring the Significance of Irrational Numbers
The square root of 24, being an irrational number, provides a glimpse into a broader mathematical concept: the vastness of irrational numbers. While rational numbers can be easily expressed as fractions, irrational numbers challenge our intuitive understanding of numbers, revealing the intricacies and complexities within the number system.
The existence of irrational numbers was a significant discovery in the history of mathematics, forever altering our perception of numbers and their relationships. Their presence highlights the infinite nature of numbers and the limitations of representing all numbers using simple ratios. Understanding irrational numbers, therefore, is not merely about calculating approximations; it's about appreciating the fundamental nature of the number system.
Conclusion: Embracing the Irrational
The square root of 24, while seemingly a simple concept, opens doors to a deeper understanding of square roots, irrational numbers, and their wide-ranging applications. From simplifying expressions to employing numerical methods, mastering this concept enhances our mathematical abilities and provides us with tools for solving various problems across diverse fields. Understanding and appreciating irrational numbers, exemplified by √24, deepens our appreciation for the elegance and complexity of mathematics. This exploration serves as a reminder that while we might not always find neat, whole-number answers, the journey of discovery and the application of mathematical principles are just as important.
Latest Posts
Latest Posts
-
In Which Hemisphere India Is Located
Mar 31, 2025
-
Worksheet On Passive And Active Voice
Mar 31, 2025
-
A Piece Of Land Surrounded By Water On Three Sides
Mar 31, 2025
-
How Far Is 20 Kilometers In Miles
Mar 31, 2025
-
How To Find The Perimeter Of Semicircle
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What The Square Root Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
