What Is 25 Percent Of 150
Juapaving
Mar 28, 2025 · 5 min read
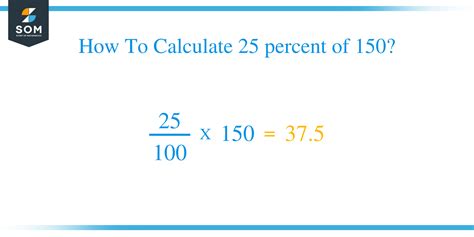
Table of Contents
What is 25 Percent of 150? A Deep Dive into Percentage Calculations
Finding 25% of 150 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for various applications in everyday life, from calculating discounts and taxes to understanding statistics and financial data. This article will not only answer the question directly but will also explore the different methods to solve this and similar problems, delving into the conceptual understanding of percentages and providing practical examples.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25. Understanding this fundamental concept is key to performing any percentage calculation.
Method 1: Using the Fraction Method
This is perhaps the most intuitive method, especially for smaller percentages like 25%. Since 25% is equivalent to ¼ (25/100 simplifies to 1/4), finding 25% of 150 is the same as finding ¼ of 150.
The calculation:
150 x (1/4) = 150/4 = 37.5
Therefore, 25% of 150 is 37.5.
This method is particularly useful for percentages that have easy fractional equivalents, like 50% (1/2), 10% (1/10), and 75% (3/4).
Method 2: Using Decimal Conversion
This method involves converting the percentage to its decimal equivalent and then multiplying it by the number. To convert a percentage to a decimal, simply divide it by 100.
The calculation:
- Convert 25% to a decimal: 25/100 = 0.25
- Multiply the decimal by the number: 0.25 x 150 = 37.5
Therefore, 25% of 150 is 37.5.
This method is versatile and works for any percentage, regardless of its fractional equivalent. It's often preferred for more complex percentage calculations involving decimals or larger percentages.
Method 3: Using Proportions
This method is based on setting up a proportion to solve for the unknown value. A proportion is an equation stating that two ratios are equal.
The setup:
We can set up a proportion as follows:
25/100 = x/150
Where 'x' represents 25% of 150.
Solving the proportion:
To solve for x, we can cross-multiply:
25 * 150 = 100 * x
3750 = 100x
x = 3750/100
x = 37.5
Therefore, 25% of 150 is 37.5.
The proportion method is a powerful tool for solving various percentage problems, especially those involving more complex relationships between percentages and quantities.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is essential in numerous real-world situations. Here are some examples:
1. Sales and Discounts:
Retail stores frequently offer discounts expressed as percentages. If a shirt is originally priced at $150 and is on sale for 25% off, you can use the methods discussed above to calculate the discount amount ($37.5) and the final price ($150 - $37.5 = $112.5).
2. Taxes:
Sales tax is often expressed as a percentage of the purchase price. If the sales tax in your area is 6%, you'd calculate 6% of the pre-tax price to determine the amount of tax owed.
3. Tips and Gratuities:
When dining out, it's customary to leave a tip, usually expressed as a percentage of the bill. Calculating 20% of the bill, for example, would determine the appropriate tip amount.
4. Financial Calculations:
Percentages are integral to financial planning and analysis. Calculating interest rates on loans, determining investment returns, or understanding profit margins all involve percentage calculations.
5. Statistics and Data Analysis:
Percentages are frequently used to represent data in charts, graphs, and reports. Understanding percentages allows for accurate interpretation of data and identification of trends.
6. Scientific Applications:
In many scientific fields, percentages are used to express concentrations, error rates, or changes in variables.
Expanding on Percentage Calculations: More Complex Scenarios
While finding 25% of 150 is relatively straightforward, let's explore more complex scenarios to further enhance our understanding:
Finding X% of Y: A General Formula
The general formula for finding X% of Y is:
(X/100) * Y = Result
This formula works for any values of X and Y.
Calculating the Percentage Increase or Decrease
This involves determining the percentage change between two numbers. The formula is:
((New Value - Original Value) / Original Value) * 100% = Percentage Change
A positive result indicates an increase, while a negative result indicates a decrease.
Calculating the Original Value Before a Percentage Change
If you know the final value after a percentage change, you can work backward to find the original value. This often requires algebraic manipulation of the percentage change formula.
Advanced Percentage Problems and Solutions
Let's consider some slightly more challenging problems involving percentages:
Problem 1: A product costs $150 after a 25% discount. What was the original price?
Solution: Let's denote the original price as 'P'. After a 25% discount, the price is 75% of the original price (100% - 25% = 75%). Therefore:
0.75P = $150
P = $150 / 0.75
P = $200
The original price was $200.
Problem 2: If 150 represents 25% of a total quantity, what is the total quantity?
Solution: Let the total quantity be 'T'. We can set up a proportion:
25/100 = 150/T
Cross-multiplying:
25T = 15000
T = 15000/25
T = 600
The total quantity is 600.
Conclusion: Mastering Percentage Calculations for Success
Understanding and mastering percentage calculations is a valuable skill applicable across various aspects of life. From everyday purchases and financial planning to data analysis and scientific applications, the ability to accurately calculate percentages enables informed decision-making and a deeper understanding of quantitative information. By employing different methods and practicing with various scenarios, you can build confidence and proficiency in this essential mathematical skill. Remember to choose the method that best suits the specific problem and always double-check your work to ensure accuracy. The examples and problems provided in this article offer a comprehensive guide to help you navigate the world of percentages with confidence.
Latest Posts
Latest Posts
-
Worksheet On Passive And Active Voice
Mar 31, 2025
-
A Piece Of Land Surrounded By Water On Three Sides
Mar 31, 2025
-
How Far Is 20 Kilometers In Miles
Mar 31, 2025
-
How To Find The Perimeter Of Semicircle
Mar 31, 2025
-
What Is The Least Common Multiple Of 11 And 2
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
