The Diagonals Of An Isosceles Trapezoid Are Congruent
Juapaving
Mar 21, 2025 · 5 min read
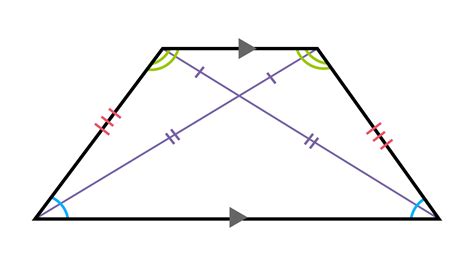
Table of Contents
- The Diagonals Of An Isosceles Trapezoid Are Congruent
- Table of Contents
- The Diagonals of an Isosceles Trapezoid are Congruent: A Comprehensive Exploration
- Understanding Isosceles Trapezoids
- Key Characteristics of Isosceles Trapezoids
- Proving the Congruence of Diagonals
- Method 1: Using Congruent Triangles
- Method 2: Utilizing Auxiliary Lines
- Method 3: Vector Approach (Advanced)
- Applications of the Theorem
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
The Diagonals of an Isosceles Trapezoid are Congruent: A Comprehensive Exploration
The world of geometry often unveils elegant properties and relationships within seemingly simple shapes. One such captivating relationship exists within the isosceles trapezoid: its diagonals are congruent. This seemingly straightforward statement underpins a wealth of geometric principles and serves as a cornerstone for solving numerous problems. This article delves into a comprehensive exploration of this theorem, proving its validity through multiple approaches and showcasing its practical applications.
Understanding Isosceles Trapezoids
Before embarking on the proof, let's solidify our understanding of the key player: the isosceles trapezoid. An isosceles trapezoid is a quadrilateral with at least one pair of parallel sides (the bases) and two non-parallel sides (the legs) of equal length. This definition is crucial because it sets the stage for the unique properties that distinguish isosceles trapezoids from other quadrilaterals.
Key Characteristics of Isosceles Trapezoids
- Parallel Bases: The two parallel sides are fundamentally defining characteristics. They dictate the trapezoidal nature of the shape.
- Congruent Legs: The equal length of the non-parallel sides is what distinguishes an isosceles trapezoid from a general trapezoid. This equality is pivotal to the congruence of the diagonals.
- Congruent Base Angles: A significant consequence of the equal legs is that the base angles (angles formed by a base and a leg) are congruent. This means that the angles at each end of a base are equal in measure. This property is frequently used in proofs.
- Supplementary Adjacent Angles: Like all trapezoids, consecutive angles along the same leg are supplementary, meaning their sum is 180 degrees. This supplementary relationship holds true even with the isosceles variation.
Proving the Congruence of Diagonals
The core of this article revolves around proving the theorem: the diagonals of an isosceles trapezoid are congruent. We will explore several methods to demonstrate this property, each offering a unique perspective on the underlying geometry.
Method 1: Using Congruent Triangles
This approach leverages the power of congruent triangles to establish the congruence of the diagonals.
1. Construction: Consider an isosceles trapezoid ABCD, where AB || CD (AB and CD are the parallel bases) and AD = BC (AD and BC are the congruent legs). Draw the diagonals AC and BD.
2. Triangle Formation: We now focus on creating congruent triangles. Consider triangles ABD and ABC. They share a common side (AB). Since AD = BC (given), and AB = AB (reflexive property), we have two sides equal.
3. Establishing Congruence: We need one more piece of information to prove congruence. Notice that angles DAB and ABC are congruent base angles of the isosceles trapezoid. Therefore, by the Side-Angle-Side (SAS) congruence postulate, we conclude that ΔABD ≅ ΔBAC.
4. Congruent Diagonals: Since ΔABD ≅ ΔBAC, the corresponding sides AC and BD are congruent. This proves that the diagonals of the isosceles trapezoid are congruent.
Method 2: Utilizing Auxiliary Lines
This method employs the construction of auxiliary lines to create congruent triangles, providing an alternative pathway to the proof.
1. Construction: Again, consider isosceles trapezoid ABCD with AB || CD and AD = BC. Draw altitudes from A and B to CD, meeting CD at E and F respectively.
2. Rectangle Formation: AEFB is a rectangle because AE and BF are altitudes, and AB is parallel to CD. Consequently, AE = BF and EF = AB.
3. Congruent Right Triangles: Consider right triangles ADE and BCF. We know that AD = BC (given) and AE = BF (from the rectangle). Using the Pythagorean theorem, we can show that DE = CF. Therefore, by the Hypotenuse-Leg (HL) postulate for right-angled triangles, ΔADE ≅ ΔBCF.
4. Congruent Segments: Since ΔADE ≅ ΔBCF, we have DE = CF. This means that CE = DF.
5. Congruent Triangles (Again!): Now consider triangles ACD and BDC. They share the side CD. Also, AD = BC and CE = DF. Using the Side-Side-Side (SSS) congruence postulate, we establish that ΔACD ≅ ΔBCD.
6. Congruent Diagonals (Conclusion): Since ΔACD ≅ ΔBCD, their corresponding sides AC and BD are congruent. Therefore, the diagonals of the isosceles trapezoid are congruent.
Method 3: Vector Approach (Advanced)
For those comfortable with vector notation, this method provides a concise and elegant proof.
1. Vector Representation: Let's represent the vertices of the trapezoid using vectors: A = a, B = b, C = c, D = d.
2. Parallel Condition: Since AB || CD, the vector AB is parallel to the vector CD. This means that b - a = k(c - d) for some scalar k.
3. Isosceles Condition: Since AD = BC, the magnitude of the vectors AD and BC are equal: |d - a| = |c - b|.
4. Diagonal Vectors: The diagonals are represented by the vectors AC = c - a and BD = d - b.
5. Proof by Magnitude Equality: Through vector manipulation and application of the isosceles condition, it can be shown that |c - a|² = |d - b|². This implies |c - a| = |d - b|, meaning the magnitudes of the diagonal vectors are equal, hence the diagonals are congruent. (Detailed vector algebra is beyond the scope of this article but can be found in advanced geometry texts).
Applications of the Theorem
The congruence of diagonals in an isosceles trapezoid isn't merely a theoretical curiosity; it has practical applications in various fields:
- Engineering and Construction: This property finds use in structural design, ensuring symmetry and stability in constructions involving trapezoidal elements.
- Computer Graphics: In computer-aided design (CAD) and computer graphics, understanding this property aids in creating accurate and symmetrical representations of trapezoidal structures.
- Cartography: Mapmaking often involves trapezoidal approximations of geographical regions, and the diagonal property assists in maintaining accuracy and consistency.
- Problem Solving in Geometry: The theorem is frequently applied in solving geometric problems, particularly those involving proving congruence or calculating lengths and angles within trapezoids.
Conclusion
The theorem stating that the diagonals of an isosceles trapezoid are congruent is a fundamental result in geometry. This article has explored multiple proof methods, showcasing the versatility and elegance of this property. Understanding this theorem is not just about memorizing a fact; it's about grasping the underlying geometric relationships and appreciating the power of congruent triangles and vector analysis. The practical applications of this seemingly simple geometric property underscore its significance across various disciplines, solidifying its position as a cornerstone of geometric understanding. Further exploration into related theorems and their applications can deepen one's understanding and appreciation for the rich world of geometric principles.
Latest Posts
Latest Posts
-
The Shapes Of The Horizontal Cross Sections
Mar 28, 2025
-
The Largest Gland Of The Body
Mar 28, 2025
-
What Is The Lcm Of 6 8 And 9
Mar 28, 2025
-
If The Diagonals Of A Quadrilateral Bisect Each Other
Mar 28, 2025
-
Write The Electron Configuration For A Neutral Atom Of Magnesium
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about The Diagonals Of An Isosceles Trapezoid Are Congruent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
