What Is The Lcm Of 6 8 And 9
Juapaving
Mar 28, 2025 · 5 min read
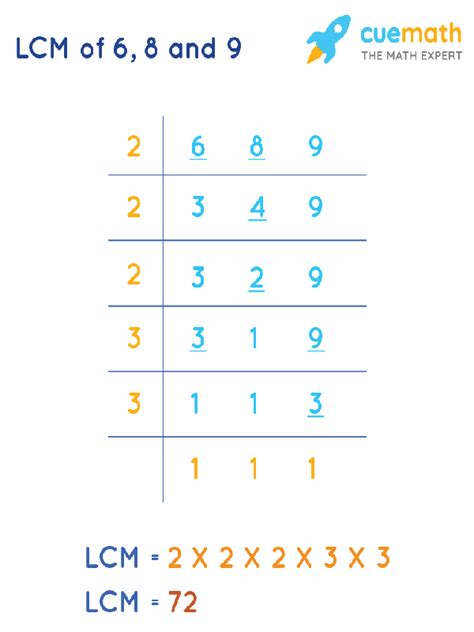
Table of Contents
What is the LCM of 6, 8, and 9? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to scheduling events. This article will comprehensively explore how to calculate the LCM of 6, 8, and 9, delving into different methods and highlighting the underlying mathematical principles. We'll also explore the broader context of LCMs and their practical uses.
Understanding Least Common Multiples (LCM)
Before diving into the specific calculation for 6, 8, and 9, let's solidify our understanding of LCMs. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors.
Key Characteristics of LCM:
- Positive Integer: The LCM is always a positive integer.
- Divisibility: The LCM is divisible by each of the given numbers.
- Smallest Value: It's the smallest number that satisfies the divisibility condition.
Methods for Finding the LCM of 6, 8, and 9
There are several methods to determine the LCM, each with its own advantages and disadvantages. We'll explore three common approaches: listing multiples, prime factorization, and using the greatest common divisor (GCD).
1. Listing Multiples Method
This is the most straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 72, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, ...
By examining the lists, we can see that the smallest number present in all three lists is 72. Therefore, the LCM of 6, 8, and 9 is 72.
This method becomes less efficient with larger numbers as the lists grow significantly.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the highest powers of all prime factors present.
- Prime factorization of 6: 2 x 3
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3² = 9
Now, multiply these highest powers together: 8 x 9 = 72. Thus, the LCM of 6, 8, and 9 is 72.
This method is generally preferred for its efficiency and systematic approach, especially when dealing with larger numbers.
3. Using the Greatest Common Divisor (GCD) Method
This method leverages the relationship between LCM and GCD. The LCM and GCD of two numbers are related by the formula:
LCM(a, b) x GCD(a, b) = a x b
While this formula is directly applicable for two numbers, it can be extended for multiple numbers by applying it iteratively. First, find the GCD of two numbers, then find the LCM of the result and the third number, and so on.
Let's illustrate this with 6, 8, and 9.
-
Find the GCD of 6 and 8: The GCD(6, 8) = 2
-
Find the LCM of 6 and 8: Using the formula, LCM(6, 8) = (6 x 8) / GCD(6, 8) = (48) / 2 = 24
-
Find the GCD of 24 and 9: The GCD(24, 9) = 3
-
Find the LCM of 24 and 9: Using the formula, LCM(24, 9) = (24 x 9) / GCD(24, 9) = (216) / 3 = 72
Therefore, the LCM of 6, 8, and 9 is 72.
This method is also efficient, especially when dealing with larger numbers, though it might require multiple steps for more than two numbers.
Applications of LCM
The concept of LCM extends far beyond simple mathematical exercises. It finds practical applications in various fields:
-
Scheduling: Determining the time when events will occur simultaneously. For instance, if three buses depart at different intervals, the LCM can calculate when they will depart together again.
-
Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is simply the LCM of the denominators.
-
Calendars: Calculating the time when specific days of the week coincide (e.g., when a specific date falls on a particular day of the week).
-
Music: In music theory, the LCM is used to determine the least common denominator of time signatures in musical composition.
-
Engineering: LCM is used in gear ratios and other mechanical systems to synchronize components.
Conclusion: The LCM of 6, 8, and 9 is 72
Through various methods, we have conclusively determined that the least common multiple of 6, 8, and 9 is 72. Understanding the different approaches—listing multiples, prime factorization, and using the GCD—provides a versatile toolkit for calculating LCMs in diverse scenarios. Remember, choosing the most efficient method depends on the context and the size of the numbers involved. The applications of LCM extend beyond basic arithmetic, impacting various real-world situations. Mastering this concept is a crucial step in solidifying your mathematical foundation and tackling more complex problems. The ability to efficiently calculate the LCM opens up a broader understanding of mathematical relationships and their practical implications.
Latest Posts
Latest Posts
-
What Is The Lcm Of 3 4 And 5
Mar 31, 2025
-
Is Cooking Food A Chemical Change
Mar 31, 2025
-
Describe Rutherfords Model Of An Atom
Mar 31, 2025
-
Plants Exchange Gas With The Atmosphere
Mar 31, 2025
-
Numbers In Words 1 To 1000000
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 6 8 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
