If The Diagonals Of A Quadrilateral Bisect Each Other
Juapaving
Mar 28, 2025 · 5 min read
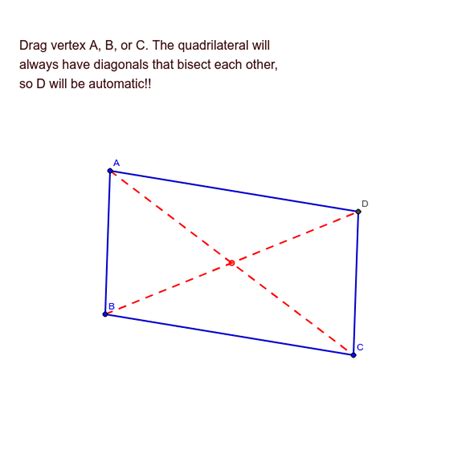
Table of Contents
If the Diagonals of a Quadrilateral Bisect Each Other
The properties of quadrilaterals are a cornerstone of geometry, providing a rich field of exploration for mathematicians and students alike. One particularly interesting characteristic involves the diagonals of a quadrilateral and their behavior when they bisect each other. This exploration delves into the implications of this property, examining its significance, proving its central theorem, and exploring its applications in various geometric problems.
Understanding the Theorem: A Foundation of Quadrilateral Geometry
The central theorem we'll be investigating states: If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram. This seemingly simple statement holds significant weight in geometric proofs and problem-solving. Let's unpack this theorem, understanding its implications and its converse.
The Significance of the Theorem
This theorem provides a crucial link between the properties of diagonals and the classification of quadrilaterals. It offers a straightforward way to identify a parallelogram based solely on the behavior of its diagonals. This is incredibly useful in various mathematical contexts, from proving other geometric relationships to solving practical problems involving shapes and areas.
The Converse of the Theorem: Equally Important
It's equally important to understand the converse of this theorem: If a quadrilateral is a parallelogram, then its diagonals bisect each other. This statement, while seemingly obvious to those familiar with parallelogram properties, forms the bedrock for understanding why the original theorem holds true. The two theorems are essentially two sides of the same coin, reinforcing each other's validity.
Proving the Theorem: A Step-by-Step Approach
The proof of the theorem "If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram" relies on fundamental geometric principles and congruent triangles. Let's consider a quadrilateral ABCD, where the diagonals AC and BD bisect each other at point O. We need to prove that ABCD is a parallelogram.
1. Establishing Congruent Triangles:
We start by examining triangles ΔAOB and ΔCOD. Since the diagonals bisect each other, we know the following:
- AO = OC (Diagonals bisect each other)
- BO = OD (Diagonals bisect each other)
- ∠AOB = ∠COD (Vertically opposite angles are equal)
Based on the Side-Angle-Side (SAS) congruence postulate, we can conclude that ΔAOB ≅ ΔCOD.
2. Establishing Parallel Sides:
From the congruence of ΔAOB and ΔCOD, we deduce the following:
- AB = CD (Corresponding sides of congruent triangles are equal)
- ∠OAB = ∠OCD (Corresponding angles of congruent triangles are equal)
Since ∠OAB and ∠OCD are alternate interior angles, and they are equal, we can conclude that AB || CD.
3. Repeating the Process:
We now repeat the same process for triangles ΔBOC and ΔDOA. Again, using the SAS congruence postulate, we find that ΔBOC ≅ ΔDOA. This leads to:
- BC = DA (Corresponding sides of congruent triangles are equal)
- ∠OBC = ∠ODA (Corresponding angles of congruent triangles are equal)
Again, since ∠OBC and ∠ODA are alternate interior angles, and they are equal, we can conclude that BC || DA.
4. Defining a Parallelogram:
Having established that AB || CD and BC || DA, we fulfill the definition of a parallelogram: A quadrilateral is a parallelogram if and only if both pairs of opposite sides are parallel. Therefore, we have successfully proven that if the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
Applications and Further Explorations
The theorem regarding bisecting diagonals is not merely an abstract geometric concept; it finds practical applications in various areas. Let's explore some of these applications:
Problem Solving in Geometry
This theorem is invaluable in solving numerous geometric problems. For instance, if you're given a quadrilateral with bisecting diagonals and asked to prove other properties (like equality of angles or sides), knowing it's a parallelogram simplifies the problem considerably. You can leverage the already established properties of parallelograms to reach the solution more efficiently.
Applications in Engineering and Construction
The concept of parallelograms, directly linked to this theorem, is fundamental in engineering and construction. Understanding the properties of parallelograms, including those derived from the diagonal bisection theorem, is crucial in designing stable and structurally sound frameworks. For instance, analyzing the stability of a bridge truss involves understanding the forces acting on parallelogram-shaped components.
Coordinate Geometry
In coordinate geometry, the theorem can be used to determine if a quadrilateral formed by four points is a parallelogram. By calculating the midpoints of the diagonals, we can readily check if they coincide. If they do, then the quadrilateral is a parallelogram. This provides a powerful tool for verifying geometric properties using algebraic methods.
Beyond Parallelograms: Other Quadrilaterals and Their Diagonals
While this theorem focuses on parallelograms, it's essential to understand how diagonals behave in other types of quadrilaterals. Let's briefly examine this:
Rectangles, Rhombuses, and Squares
In rectangles, rhombuses, and squares (all of which are parallelograms), the diagonals bisect each other, but they also exhibit additional properties:
- Rectangles: Diagonals are equal in length.
- Rhombuses: Diagonals are perpendicular bisectors of each other.
- Squares: Diagonals are equal in length, perpendicular bisectors of each other, and bisect the angles of the square.
Trapezoids and Irregular Quadrilaterals
In trapezoids and irregular quadrilaterals, the diagonals generally do not bisect each other. This lack of bisection differentiates these quadrilaterals from parallelograms and highlights the special property of parallelograms possessing bisecting diagonals. Analyzing the behavior of diagonals helps categorize and understand the diverse family of quadrilaterals.
Conclusion: A Cornerstone of Geometric Understanding
The theorem stating that if the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram, serves as a fundamental concept in geometry. Its proof, reliant on congruent triangles and the definition of a parallelogram, elegantly connects different geometric concepts. The theorem's applications extend beyond theoretical explorations, finding practical use in problem-solving, engineering, and coordinate geometry. Understanding this theorem and its implications deepens one's appreciation of the rich tapestry of geometric relationships. It's a cornerstone of geometric understanding, providing a powerful tool for classifying and analyzing quadrilaterals and their properties. Its importance lies not only in its simplicity but also in its power to unlock a deeper understanding of the world of shapes and their inherent characteristics. Further exploration into the properties of quadrilaterals and their diagonals will undoubtedly continue to yield exciting insights into the fascinating world of geometry.
Latest Posts
Latest Posts
-
54 As Product Of Prime Factors
Mar 31, 2025
-
Organelles That Are The Sites Of Protein Synthesis
Mar 31, 2025
-
What Is The Percentage Of 2 5
Mar 31, 2025
-
How To Find Reciprocal Of A Mixed Number
Mar 31, 2025
-
Which Of The Following Is Considered A Micronutrient
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about If The Diagonals Of A Quadrilateral Bisect Each Other . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
