Least Common Multiple Of 8 10
Juapaving
Mar 26, 2025 · 5 min read
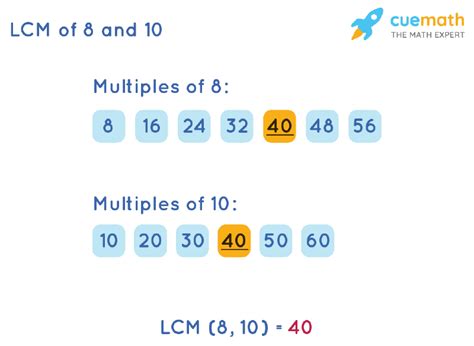
Table of Contents
Finding the Least Common Multiple (LCM) of 8 and 10: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to calculate the LCM is crucial for various applications, from simplifying fractions to solving problems in algebra and beyond. This article will delve deep into finding the LCM of 8 and 10, exploring multiple methods and illustrating the underlying principles. We'll also touch upon the broader significance of LCMs and their practical uses.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3. This concept extends to more than two integers as well.
Methods for Calculating the LCM of 8 and 10
There are several effective methods to determine the LCM of two numbers, 8 and 10 in this case. Let's explore the most common approaches:
1. Listing Multiples Method
This is a straightforward, intuitive method, especially useful for smaller numbers. We simply list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100...
By comparing the lists, we observe that the smallest multiple appearing in both sequences is 40. Therefore, the LCM of 8 and 10 is 40.
This method is effective for smaller numbers but can become cumbersome for larger numbers.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 10: 2 x 5
To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together.
- The prime factors are 2 and 5.
- The highest power of 2 is 2³ = 8.
- The highest power of 5 is 5¹ = 5.
Therefore, LCM(8, 10) = 2³ x 5 = 8 x 5 = 40.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. That is:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 8 and 10. We can use the Euclidean algorithm for this:
- Divide the larger number (10) by the smaller number (8): 10 ÷ 8 = 1 with a remainder of 2.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (2): 8 ÷ 2 = 4 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 2.
Now, we can use the formula:
LCM(8, 10) = (8 x 10) / GCD(8, 10) = (80) / 2 = 40
This method is particularly useful when dealing with larger numbers, as finding the GCD is often easier than directly finding the LCM.
Applications of LCM
The least common multiple finds applications in numerous areas, including:
1. Fraction Arithmetic
Finding a common denominator when adding or subtracting fractions requires calculating the LCM of the denominators. For example, to add 1/8 and 1/10, we find the LCM of 8 and 10 (which is 40), and then rewrite the fractions with a denominator of 40 before adding them.
2. Scheduling Problems
LCMs are crucial for solving problems related to scheduling events that occur at regular intervals. For example, if two buses depart from a station at different intervals, the LCM of those intervals determines when both buses will depart simultaneously again.
3. Cyclic Patterns
Many real-world phenomena exhibit cyclic patterns. Determining when these cycles coincide often involves calculating the LCM. Think of planetary alignments, repeating patterns in nature, or even the synchronization of machines in a manufacturing process.
4. Music Theory
In music theory, LCMs are used in calculating the least common denominator of rhythmic patterns, helping in understanding and composing complex musical structures.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For example, to find the LCM of 8, 10, and 12, we can use the prime factorization method:
- Prime factorization of 8: 2³
- Prime factorization of 10: 2 x 5
- Prime factorization of 12: 2² x 3
The LCM would be 2³ x 3 x 5 = 120. The GCD method can also be adapted to handle multiple numbers using extensions of the Euclidean algorithm.
Conclusion: The Importance of Understanding LCM
The least common multiple is a fundamental concept with far-reaching applications across various mathematical fields and practical scenarios. Mastering the different methods for calculating the LCM, from listing multiples to prime factorization and the GCD method, equips you with a powerful tool for problem-solving in diverse contexts. Understanding the LCM allows for efficient calculations, insightful analyses of repeating patterns, and the ability to tackle complex problems effectively. Whether you're simplifying fractions, scheduling events, or exploring rhythmic patterns, the LCM provides the key to unlocking solutions and understanding the underlying mathematical relationships. This understanding fosters a deeper appreciation for the interconnectedness of mathematical concepts and their practical significance in everyday life. The simple example of finding the LCM of 8 and 10 serves as a gateway to a more comprehensive understanding of number theory and its applications.
Latest Posts
Latest Posts
-
Whats The Prime Factorization Of 15
Mar 29, 2025
-
37 Inches Is How Many Feet
Mar 29, 2025
-
Find The Lcm Of 3 And 5
Mar 29, 2025
-
How Do You Do Average In Math
Mar 29, 2025
-
Liquids At Room Temperature Periodic Table
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 8 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
