Lcm Of 2 7 And 3
Juapaving
Mar 26, 2025 · 6 min read
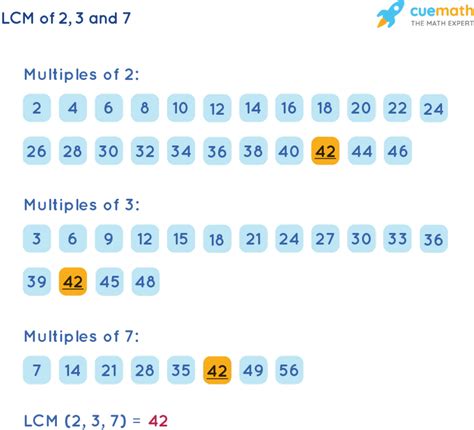
Table of Contents
Understanding the Least Common Multiple (LCM) of 2, 7, and 3
The Least Common Multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. It finds applications in various areas, from simplifying fractions to solving problems involving cyclical events. This comprehensive article will delve into the LCM, focusing specifically on finding the LCM of 2, 7, and 3, and exploring various methods to achieve this. We'll also look at the broader context of LCMs and their practical uses.
What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. For example, the LCM of 2 and 3 is 6, because 6 is the smallest positive integer that is divisible by both 2 and 3.
Why is the LCM Important?
Understanding LCMs is crucial for several reasons:
-
Simplifying Fractions: Finding the LCM of the denominators is essential when adding or subtracting fractions with different denominators. It allows you to find a common denominator, making the calculation much easier.
-
Solving Problems Involving Cycles: LCMs are used to solve problems where events repeat at regular intervals. For instance, if two machines operate on cycles of different lengths, the LCM determines when they will both be at the starting point of their cycles simultaneously.
-
Understanding Number Theory: LCMs play a significant role in number theory, forming the basis for many advanced concepts and theorems.
-
Real-world Applications: From scheduling tasks to calculating the timing of synchronized events, LCMs have practical applications in various fields.
Finding the LCM of 2, 7, and 3: Different Methods
Now, let's focus on finding the LCM of 2, 7, and 3. We'll explore several methods to illustrate the concept and provide flexibility in approach.
Method 1: Listing Multiples
The simplest method, suitable for smaller numbers, involves listing the multiples of each number until a common multiple is found.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 21, 22, 24, 26, 28, 30, ...
- Multiples of 7: 7, 14, 21, 28, 35, 42, ...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ...
By examining the lists, we can see that the smallest common multiple is 42. Therefore, the LCM(2, 7, 3) = 42.
This method becomes cumbersome for larger numbers.
Method 2: Prime Factorization
This is a more efficient method, particularly for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
-
Find the prime factorization of each number:
- 2 = 2¹
- 7 = 7¹
- 3 = 3¹
-
Identify the highest power of each prime factor:
- The prime factors are 2, 3, and 7. Each appears only to the first power.
-
Multiply the highest powers together:
- LCM(2, 7, 3) = 2¹ × 3¹ × 7¹ = 42
This method is more efficient and systematic than listing multiples, making it suitable for larger numbers.
Method 3: Using the Formula (for two numbers)
While this formula directly applies to only two numbers, we can use it iteratively. The formula is:
LCM(a, b) = (|a × b|) / GCD(a, b)
where GCD is the Greatest Common Divisor.
Let's first find the LCM of 2 and 3:
- GCD(2, 3) = 1 (since 2 and 3 share no common factors other than 1)
- LCM(2, 3) = (2 × 3) / 1 = 6
Now let's find the LCM of 6 and 7:
- GCD(6, 7) = 1
- LCM(6, 7) = (6 × 7) / 1 = 42
Therefore, LCM(2, 7, 3) = 42. This method involves multiple steps, but showcases the relationship between LCM and GCD.
The Importance of Prime Factorization in Finding LCMs
The prime factorization method highlighted above is particularly powerful and efficient for finding the LCM of larger sets of numbers. Let's illustrate its power with a slightly more complex example.
Let's find the LCM of 12, 18, and 30.
-
Find the prime factorization of each number:
- 12 = 2² × 3¹
- 18 = 2¹ × 3²
- 30 = 2¹ × 3¹ × 5¹
-
Identify the highest power of each prime factor:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3² = 9
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers together:
- LCM(12, 18, 30) = 2² × 3² × 5¹ = 4 × 9 × 5 = 180
This example demonstrates how the prime factorization method efficiently handles larger numbers and multiple prime factors. It provides a systematic approach that avoids the trial-and-error nature of listing multiples.
LCM and GCD: The Inseparable Duo
The Least Common Multiple (LCM) and the Greatest Common Divisor (GCD) are intimately related. They are often used together in solving mathematical problems. Their relationship can be expressed mathematically as:
For any two positive integers 'a' and 'b':
LCM(a, b) × GCD(a, b) = a × b
This formula highlights the inverse relationship between the LCM and GCD. Knowing one allows you to easily calculate the other.
Practical Applications of LCM
The applications of LCM extend beyond the realm of pure mathematics. Here are a few examples:
-
Scheduling: Imagine you have two buses that depart from a station at regular intervals. One departs every 15 minutes, and the other every 20 minutes. The LCM(15, 20) = 60 minutes, meaning the buses will depart simultaneously again after 60 minutes (1 hour).
-
Manufacturing: In a factory setting, machines might operate on different cycles. Understanding the LCM of their cycle times helps in scheduling maintenance and optimizing production flow.
-
Music: In music theory, the LCM is crucial in understanding rhythmic patterns and harmonies.
-
Calendars: Determining when specific dates will coincide (e.g., a particular day of the week falling on a particular date) often involves using the LCM.
-
Fractions: As previously mentioned, finding the LCM of denominators is fundamental to adding and subtracting fractions.
Conclusion: Mastering the LCM
The Least Common Multiple is a fundamental mathematical concept with wide-ranging applications. While the simplest method of finding the LCM involves listing multiples, the prime factorization method is more efficient and adaptable to larger numbers. Understanding the relationship between the LCM and GCD enhances problem-solving capabilities. By mastering the LCM, you equip yourself with a valuable tool applicable across various fields, from simple arithmetic to complex mathematical problems and practical scheduling scenarios. The ability to efficiently calculate the LCM significantly streamlines processes and improves understanding in numerous areas.
Latest Posts
Latest Posts
-
What Is The Multiple Of 32
Mar 29, 2025
-
Is Cellulose A Polymer Of Glucose
Mar 29, 2025
-
Which Of The Following Do Yeast Produce During Fermentation
Mar 29, 2025
-
What Is The Chemical Formula Of Phosphorus Pentachloride
Mar 29, 2025
-
What Causes The Periodicity In The Periodic Table
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 7 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
