What Is The Multiple Of 32
Juapaving
Mar 29, 2025 · 5 min read
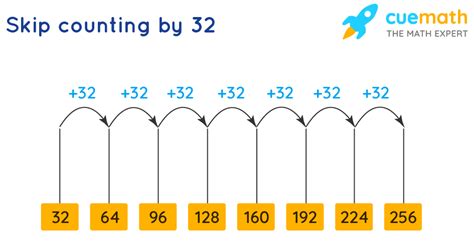
Table of Contents
What is a Multiple of 32? A Deep Dive into Multiplication and Number Theory
Understanding multiples is a fundamental concept in mathematics, forming the bedrock for more advanced topics like algebra, calculus, and number theory. This article delves deep into the concept of multiples, specifically focusing on multiples of 32. We'll explore different ways to identify them, their properties, and their applications in various fields. We’ll also touch upon related mathematical concepts to provide a comprehensive understanding.
Defining Multiples
A multiple of a number is the result of multiplying that number by any integer (whole number). For example, multiples of 5 include 5 (5 x 1), 10 (5 x 2), 15 (5 x 3), 20 (5 x 4), and so on. The integers used in the multiplication are often referred to as factors. Therefore, 5, 10, 15, and 20 are all multiples of 5, and 1, 2, 3, and 4 are their corresponding factors.
Multiples of 32: A Closer Look
Applying this definition to 32, we can say that a multiple of 32 is any number obtained by multiplying 32 by an integer. This means the multiples of 32 are:
- 32 (32 x 1)
- 64 (32 x 2)
- 96 (32 x 3)
- 128 (32 x 4)
- 160 (32 x 5)
- and so on... to infinity!
The sequence continues infinitely in both positive and negative directions. Negative multiples simply represent the result of multiplying 32 by negative integers:
- -32 (32 x -1)
- -64 (32 x -2)
- -96 (32 x -3)
- and so on...
Identifying Multiples of 32
There are several ways to determine if a number is a multiple of 32:
1. Direct Division:
The most straightforward method is to divide the number by 32. If the result is a whole number (an integer), then the number is a multiple of 32. For example, if we want to check if 256 is a multiple of 32, we perform the division: 256 ÷ 32 = 8. Since 8 is an integer, 256 is a multiple of 32.
2. Factorization:
Another approach involves prime factorization. The prime factorization of 32 is 2<sup>5</sup>. If the prime factorization of a number includes 2<sup>5</sup> (or a higher power of 2), then it's a multiple of 32. Let's consider 192:
192 = 2<sup>6</sup> x 3
Since 2<sup>6</sup> contains 2<sup>5</sup>, 192 is a multiple of 32 (192 ÷ 32 = 6).
3. Patterns and Sequences:
Observe the pattern in the multiples of 32: 32, 64, 96, 128, 160... Notice the consistent increase of 32 between consecutive multiples. This pattern can be used to quickly identify potential multiples, especially within a given range.
Properties of Multiples of 32
Multiples of 32 share certain properties:
- Divisibility by 2: All multiples of 32 are divisible by 2 (because 32 itself is divisible by 2).
- Divisibility by 4: Similarly, all multiples of 32 are divisible by 4, 8, and 16.
- Even Numbers: All multiples of 32 are even numbers.
- Arithmetic Progression: The sequence of multiples of 32 forms an arithmetic progression with a common difference of 32.
Applications of Multiples of 32
The concept of multiples, and specifically multiples of 32, finds application in various fields:
1. Computer Science:
In computer science, multiples of 32 are frequently encountered due to the prevalence of 32-bit systems. Memory addressing, data structures, and image processing often involve multiples of 32 for efficient data handling. For instance, many image formats use 32-bit color depths, where each pixel requires 32 bits of information.
2. Engineering:
In engineering, multiples of 32 might be used in calculations related to measurements, dimensions, or resource allocation. For example, in designing structures, dimensions might be chosen as multiples of 32 for ease of calculation and construction.
3. Music:
While not as direct, the concept of multiples relates to musical scales and rhythms. Musical intervals and rhythmic patterns often exhibit mathematical relationships that involve multiples.
4. Everyday Life:
Even in everyday life, the concept of multiples appears implicitly. For example, if you buy items in packs of 32, the total number of items will always be a multiple of 32.
Multiples of 32 and Number Theory
Understanding multiples of 32 connects directly to several key concepts within number theory:
1. Divisibility Rules:
The concept of divisibility is closely tied to multiples. A number is divisible by another if it's a multiple of that other number. Divisibility rules help determine if a number is divisible by certain integers without performing the actual division. While there isn't a specific divisibility rule for 32, we can use divisibility rules for its factors (2, 4, 8, 16) as intermediate checks.
2. Prime Factorization:
As mentioned earlier, prime factorization helps determine if a number is a multiple of 32 by examining its prime factors. This concept is fundamental in number theory and has wide-ranging applications in cryptography and other areas.
3. Least Common Multiple (LCM):
The least common multiple (LCM) of two or more numbers is the smallest number that is a multiple of all of them. Finding the LCM is crucial in various mathematical problems and applications. If you were to find the LCM of 32 and another number, the result would always be a multiple of 32.
Expanding Your Understanding: Exploring Further Concepts
To further strengthen your understanding of multiples and related mathematical concepts, consider exploring:
- Factors and divisors: Understand the difference between factors (numbers that divide evenly into a number) and multiples (numbers that are the result of multiplying a number by an integer).
- Greatest Common Divisor (GCD): Learn how to find the greatest common divisor of two or more numbers, a concept closely related to LCM.
- Modular Arithmetic: Explore modular arithmetic, which deals with remainders after division. Understanding modular arithmetic helps in solving various mathematical puzzles and problems.
Conclusion: Mastering Multiples of 32 and Beyond
Understanding multiples of 32, or any number for that matter, is essential for building a strong foundation in mathematics. This knowledge extends beyond basic arithmetic, finding practical applications in various fields like computer science, engineering, and even music. By grasping the underlying principles and exploring related concepts, you can significantly enhance your mathematical skills and problem-solving abilities. Remember that the exploration of mathematical concepts is a continuous journey; the more you delve into it, the more you will discover the beauty and power of numbers and their relationships.
Latest Posts
Latest Posts
-
The Pitch Of A Sound Is Determined By What
Apr 01, 2025
-
Is 2 3 Less Than 1 2
Apr 01, 2025
-
Is 23 A Prime Number Or Composite
Apr 01, 2025
-
Is The Square Root Of 45 A Rational Number
Apr 01, 2025
-
Which Phase Do Chromosomes First Become Visible
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Multiple Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
