If Two Events Are Mutually Exclusive Then
Juapaving
Mar 26, 2025 · 6 min read
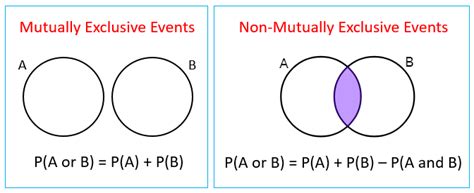
Table of Contents
If Two Events Are Mutually Exclusive, Then... Understanding Probability and its Implications
Understanding probability is crucial in many fields, from finance and insurance to medicine and engineering. A key concept within probability is that of mutually exclusive events. This article delves deep into the meaning of mutually exclusive events, explores their implications within probability calculations, and provides numerous examples to solidify your understanding. We'll also touch upon how this concept relates to other probabilistic ideas and its broader applications.
Defining Mutually Exclusive Events
Two events are considered mutually exclusive (or disjoint) if they cannot both occur at the same time. In simpler terms, the occurrence of one event completely prevents the occurrence of the other. There's no overlap between them. Think of it like flipping a coin: you can get heads or tails, but you cannot get both simultaneously.
Key characteristics of mutually exclusive events:
- No overlap: The events have no common outcomes. Their intersection is an empty set (∅).
- One event precludes the other: If one event happens, the other cannot.
- Probability of both occurring is zero: P(A and B) = 0, where A and B are the mutually exclusive events.
Understanding the Implications on Probability Calculations
The concept of mutually exclusive events significantly impacts how we calculate probabilities. The most important implication is in calculating the probability of either event occurring (the union of the two events).
The Addition Rule for Mutually Exclusive Events
The addition rule in probability states that the probability of either event A or event B occurring is:
P(A or B) = P(A) + P(B) - P(A and B)
However, because mutually exclusive events have no overlap (P(A and B) = 0), this simplifies to:
P(A or B) = P(A) + P(B)
This simplified addition rule is incredibly useful for calculating probabilities when dealing with mutually exclusive events. It allows for straightforward and efficient calculations.
Examples of Mutually Exclusive Events
Let's illustrate the concept with several real-world examples:
Example 1: Coin Toss
Consider flipping a fair coin. The events "getting heads" and "getting tails" are mutually exclusive. You cannot get both heads and tails on a single flip.
- P(Heads) = 0.5
- P(Tails) = 0.5
- P(Heads or Tails) = P(Heads) + P(Tails) = 0.5 + 0.5 = 1 (This makes sense, as you are guaranteed to get either heads or tails)
Example 2: Rolling a Die
Rolling a standard six-sided die offers another example. The events "rolling a 3" and "rolling a 6" are mutually exclusive. You cannot roll both a 3 and a 6 on a single roll.
- P(Rolling a 3) = 1/6
- P(Rolling a 6) = 1/6
- P(Rolling a 3 or a 6) = P(Rolling a 3) + P(Rolling a 6) = 1/6 + 1/6 = 1/3
Example 3: Drawing Cards from a Deck
Consider drawing a single card from a standard deck of 52 playing cards. The events "drawing a king" and "drawing a queen" are mutually exclusive. A single card cannot be both a king and a queen.
- P(Drawing a King) = 4/52 = 1/13
- P(Drawing a Queen) = 4/52 = 1/13
- P(Drawing a King or a Queen) = P(Drawing a King) + P(Drawing a Queen) = 1/13 + 1/13 = 2/13
Example 4: Weather Conditions
The events "it will rain tomorrow" and "it will be sunny tomorrow" are approximately mutually exclusive. While there could be a situation with a mix of sun and rain, it's generally considered mutually exclusive for simplicity.
Example 5: Medical Diagnosis
In medical diagnosis, consider two distinct diseases, A and B. If a patient has disease A, they cannot simultaneously have disease B (assuming they are completely distinct and non-overlapping conditions). The events "the patient has disease A" and "the patient has disease B" are mutually exclusive.
When Events Are NOT Mutually Exclusive
It's equally important to understand when events are not mutually exclusive. If events can occur simultaneously, they are not mutually exclusive. The standard addition rule (including the subtraction of the intersection) must be used in these cases.
Example: Drawing Cards Again
Consider drawing a card from a deck. The events "drawing a red card" and "drawing a king" are not mutually exclusive. You could draw a card that is both red and a king (the king of hearts or the king of diamonds).
Mutually Exclusive Events and Conditional Probability
The concept of mutually exclusive events also interacts with conditional probability. The conditional probability of event A given event B is written as P(A|B) and represents the probability of A occurring given that B has already occurred.
If A and B are mutually exclusive, then P(A|B) = 0, and P(B|A) = 0. This is because if one event has occurred, the other is impossible.
Mutually Exclusive Events and Independent Events
It's crucial to distinguish between mutually exclusive events and independent events. Two events are independent if the occurrence of one does not affect the probability of the other. Mutually exclusive events are not independent. If one mutually exclusive event occurs, it guarantees that the other will not occur.
For example, the events of rolling a 3 and rolling a 6 on a single die roll are mutually exclusive (they can’t both happen), and they are not independent (if you roll a 3, you cannot roll a 6).
Applications of Mutually Exclusive Events
Understanding mutually exclusive events has wide-ranging applications in various fields:
- Risk Assessment: In finance and insurance, assessing risks often involves identifying mutually exclusive events (e.g., different types of accidents in car insurance).
- Quality Control: In manufacturing, identifying mutually exclusive defects (e.g., cracks, scratches, mis-shapen parts) helps assess product quality.
- Medical Research: Clinical trials often involve analyzing the occurrence of mutually exclusive outcomes (e.g., success or failure of a treatment).
- Weather Forecasting: While not perfectly mutually exclusive, simplifying weather conditions (e.g., rain, snow, sunshine) into mutually exclusive categories aids in forecasting.
- Game Theory: In game theory, analyzing different outcomes as mutually exclusive events is vital in strategic decision-making.
Conclusion
The concept of mutually exclusive events is a fundamental building block in probability theory. Understanding when events are mutually exclusive is crucial for accurate probability calculations, particularly when employing the addition rule. The examples and applications provided throughout this article underscore the significance of this concept across diverse fields. By grasping this core idea, you'll strengthen your understanding of probability and its practical applications. Remember to always carefully consider whether events are truly mutually exclusive before applying the simplified addition rule; otherwise, the standard addition rule, incorporating the intersection, should be used. This careful consideration will enhance the accuracy and reliability of your probabilistic analyses.
Latest Posts
Latest Posts
-
Label The Diagram Of The Male Reproductive System
Mar 29, 2025
-
Moment Of Inertia Of A Rectangular Plate
Mar 29, 2025
-
2 Lines Cut By A Transversal
Mar 29, 2025
-
Chemical Reaction Examples In Everyday Life
Mar 29, 2025
-
Twin Primes From 1 To 100
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about If Two Events Are Mutually Exclusive Then . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
