2 Lines Cut By A Transversal
Juapaving
Mar 29, 2025 · 7 min read
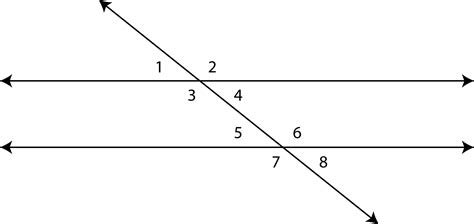
Table of Contents
When Two Lines Meet a Transversal: Exploring the Geometry of Parallel and Intersecting Lines
Geometry, the study of shapes, sizes, relative positions of figures, and the properties of space, often begins with foundational concepts. One of these fundamental concepts involves the relationship between two lines intersected by a third line, known as a transversal. Understanding how these lines interact – whether they are parallel or intersecting – is crucial to mastering many geometric theorems and solving complex problems. This comprehensive guide will delve into the intricacies of two lines cut by a transversal, exploring the resulting angles and their properties. We'll examine parallel lines, intersecting lines, and the theorems that govern their interactions, providing a solid foundation for further geometric exploration.
Understanding the Basics: Lines and Transversals
Before diving into the complexities, let's define our key terms.
-
Line: A straight one-dimensional figure extending infinitely in both directions. We often represent lines with lowercase letters (e.g., line l, line m) or by naming two points on the line (e.g., line AB).
-
Transversal: A line that intersects two or more other lines at distinct points. The transversal acts as a "cutter," creating several angles at the points of intersection.
When a transversal intersects two lines, it creates eight angles. These angles are categorized and named based on their positions relative to the two lines and the transversal. Understanding this categorization is essential for navigating the theorems that follow.
Angles Formed by a Transversal: A Detailed Breakdown
The eight angles formed when a transversal intersects two lines can be grouped into several categories:
1. Interior Angles:
These angles are located between the two lines intersected by the transversal. There are four interior angles in total.
2. Exterior Angles:
These angles are located outside the two lines intersected by the transversal. Like interior angles, there are four exterior angles.
3. Consecutive Interior Angles:
These are pairs of interior angles that lie on the same side of the transversal. There are two pairs of consecutive interior angles.
4. Alternate Interior Angles:
These are pairs of interior angles that lie on opposite sides of the transversal. They are not adjacent to each other. There are two pairs of alternate interior angles.
5. Consecutive Exterior Angles:
These are pairs of exterior angles that lie on the same side of the transversal. There are two pairs of consecutive exterior angles.
6. Alternate Exterior Angles:
These are pairs of exterior angles that lie on opposite sides of the transversal. They are not adjacent to each other. There are two pairs of alternate exterior angles.
7. Corresponding Angles:
These are pairs of angles, one interior and one exterior, that are located on the same side of the transversal and in corresponding positions relative to the two lines. There are four pairs of corresponding angles.
Parallel Lines Cut by a Transversal: The Theorems
When the two lines intersected by a transversal are parallel, specific relationships exist between the angles formed. These relationships are formalized in several important geometric theorems:
1. Corresponding Angles Postulate/Theorem:
If two parallel lines are cut by a transversal, then the corresponding angles are congruent (equal in measure). This postulate is a fundamental building block for many other theorems. This means that corresponding angles, as described above, will always have the same degree measurement when the lines are parallel.
2. Alternate Interior Angles Theorem:
If two parallel lines are cut by a transversal, then the alternate interior angles are congruent. This theorem is directly derived from the Corresponding Angles Postulate.
3. Alternate Exterior Angles Theorem:
If two parallel lines are cut by a transversal, then the alternate exterior angles are congruent. Similar to the Alternate Interior Angles Theorem, this is a direct consequence of the Corresponding Angles Postulate.
4. Consecutive Interior Angles Theorem:
If two parallel lines are cut by a transversal, then consecutive interior angles are supplementary (their measures add up to 180 degrees). This theorem highlights the relationship between angles on the same side of the transversal.
5. Consecutive Exterior Angles Theorem:
If two parallel lines are cut by a transversal, then consecutive exterior angles are supplementary. This is analogous to the Consecutive Interior Angles Theorem, but for exterior angles.
These theorems provide a powerful toolkit for solving problems involving parallel lines and transversals. By identifying the type of angle pair and applying the appropriate theorem, we can determine the measures of unknown angles.
Intersecting Lines Cut by a Transversal: A Different Perspective
When the two lines intersected by the transversal are not parallel, they will intersect at some point. The angles formed still maintain relationships, but the theorems for parallel lines do not apply. Instead, we rely on the properties of vertical angles and linear pairs.
1. Vertical Angles Theorem:
Vertical angles are the angles opposite each other when two lines intersect. The Vertical Angles Theorem states that vertical angles are always congruent. This holds true regardless of whether a transversal is involved.
2. Linear Pair Postulate:
A linear pair consists of two adjacent angles whose non-common sides form a straight line. The Linear Pair Postulate states that angles in a linear pair are supplementary (their measures add up to 180 degrees). This is a fundamental concept in understanding angle relationships in intersecting lines.
In the case of intersecting lines cut by a transversal, we can use a combination of the Vertical Angles Theorem, the Linear Pair Postulate, and the knowledge of angle relationships to determine the measures of unknown angles. However, the theorems specific to parallel lines (Corresponding Angles, Alternate Interior Angles, etc.) will not apply.
Problem Solving and Applications
Let's illustrate the application of these theorems with a few examples:
Example 1 (Parallel Lines):
Two parallel lines, line l and line m, are intersected by a transversal, line t. One of the interior angles measures 70 degrees. Find the measures of the other seven angles.
By using the theorems for parallel lines cut by a transversal, we can deduce the measures of all other angles. For example, corresponding angles are congruent, alternate interior angles are congruent, consecutive interior angles are supplementary, and so on. This allows us to systematically determine all angle measures.
Example 2 (Intersecting Lines):
Two intersecting lines are cut by a transversal. One of the angles measures 110 degrees. Find the measures of the other seven angles.
In this case, we use the Vertical Angles Theorem and the Linear Pair Postulate. Vertical angles will be equal, and angles forming a linear pair will add up to 180 degrees. This will allow us to systematically determine the measures of all the other angles.
Beyond the Basics: Extending Our Understanding
The concepts discussed here serve as a foundational stepping stone for more advanced geometric concepts. Understanding the relationships between angles formed by two lines and a transversal is crucial for:
-
Proving geometric theorems: Many geometric proofs rely on the properties of angles formed by parallel lines and transversals.
-
Solving geometric problems: Numerous geometry problems require the application of these theorems to find unknown angle measures or lengths.
-
Trigonometry: Understanding angle relationships lays the groundwork for trigonometry, which deals with the relationships between angles and sides of triangles.
-
Coordinate Geometry: The concepts of parallel and intersecting lines are fundamental to coordinate geometry, where we use algebraic methods to study geometric figures.
-
Three-dimensional Geometry: The principles extend to more complex scenarios involving three-dimensional shapes and planes.
Conclusion: A Foundation for Geometric Exploration
The intersection of two lines by a transversal is a fundamental concept in geometry. Understanding the relationships between the angles formed, especially when the lines are parallel, is essential for mastering many geometric theorems and solving a wide range of problems. The theorems presented here provide a robust toolkit for analyzing and solving geometric problems related to parallel and intersecting lines. By mastering these concepts, you build a solid foundation for further exploration in the fascinating world of geometry. This comprehensive understanding allows you to tackle more complex geometric challenges and appreciate the elegance and power of geometric reasoning. Remember to practice applying these theorems to various problems to solidify your understanding and enhance your problem-solving skills in geometry.
Latest Posts
Latest Posts
-
A To Z In Cursive Writing
Mar 31, 2025
-
What Is The Purpose Of Mitosis In Single Celled Organisms
Mar 31, 2025
-
What Is The Difference Between A Land And Sea Breeze
Mar 31, 2025
-
A Real Gas Behaves Most Like An Ideal Gas At
Mar 31, 2025
-
How Many Valence Electrons Are Found In Phosphorus
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about 2 Lines Cut By A Transversal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
