Twin Primes From 1 To 100
Juapaving
Mar 29, 2025 · 5 min read
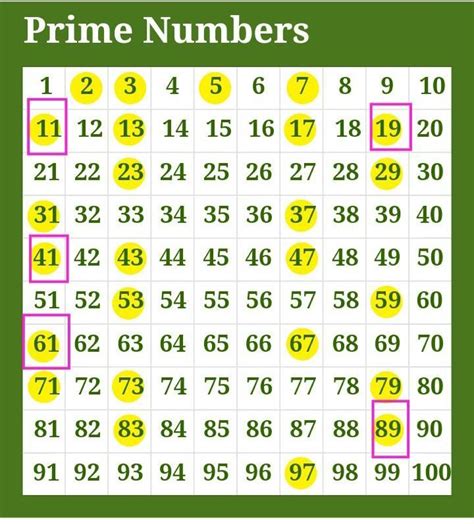
Table of Contents
Twin Primes from 1 to 100: Unveiling the Mysteries of these Number Pairs
Twin primes, a fascinating subject in number theory, captivate mathematicians and enthusiasts alike. Defined as pairs of prime numbers that differ by 2, they present a seemingly simple yet profoundly complex area of study. This article delves deep into the world of twin primes, focusing specifically on those found within the range of 1 to 100. We'll explore their properties, investigate their distribution, and touch upon the ongoing research surrounding these intriguing number pairs.
Understanding Prime and Twin Prime Numbers
Before embarking on our journey through the twin primes from 1 to 100, let's establish a firm understanding of the fundamental concepts.
What are Prime Numbers?
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In simpler terms, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. Prime numbers are the building blocks of all other numbers through factorization.
Defining Twin Primes
Twin primes are pairs of prime numbers that have a difference of 2. For example, (3, 5) and (5, 7) are twin prime pairs. The numbers in between the primes in a twin prime pair are always even. This is because one of the primes must be odd (except for the pair (3,5)), and adding 2 to an odd number always results in an odd number. The even number between the twins is always divisible by 2.
Identifying Twin Primes from 1 to 100
Now, let's embark on our quest to identify all the twin prime pairs within the range of 1 to 100. A systematic approach will be beneficial. We can list the prime numbers within this range first:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Now, let's examine consecutive pairs to identify those with a difference of 2:
- (3, 5): This is our first twin prime pair.
- (5, 7): Another twin prime pair.
- (11, 13): Here's another!
- (17, 19): Yet another pair.
- (29, 31): We continue to find them.
- (41, 43): Another successful find.
- (59, 61): Still more twin prime pairs!
- (71, 73): We're building quite a collection.
Therefore, the twin prime pairs from 1 to 100 are: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), and (71, 73). There are a total of eight twin prime pairs in this range.
The Distribution of Twin Primes: A Glimpse into the Infinite
The distribution of twin primes is a topic that has fascinated mathematicians for centuries. While they appear with some regularity in smaller ranges, their frequency decreases as we move towards larger numbers. The question of whether there are infinitely many twin primes remains one of the most challenging unsolved problems in mathematics. The Twin Prime Conjecture, which postulates that there are infinitely many twin primes, remains unproven despite significant progress in recent years.
The relative sparsity of twin primes as numbers get larger hints at the underlying complexity of their distribution. There’s no simple formula to predict where the next twin prime pair will occur; their appearance seems somewhat erratic.
Heuristic Arguments and the Prime Number Theorem
Although we can't definitively prove the Twin Prime Conjecture, heuristic arguments based on the Prime Number Theorem offer strong evidence supporting its plausibility. The Prime Number Theorem describes the asymptotic distribution of prime numbers, giving us an estimate of how many primes exist up to a given number. Similar probabilistic arguments suggest that there should be infinitely many twin primes, even though a rigorous proof remains elusive.
Advanced Concepts and Related Research
The study of twin primes extends far beyond simply identifying pairs within a specific range. Sophisticated mathematical tools and concepts are employed in ongoing research.
Brun's Theorem
Brun's Theorem, a significant result in the field, states that the sum of the reciprocals of all twin primes converges to a finite value, known as Brun's constant. This implies that while there might be infinitely many twin primes, they are relatively "sparse" compared to the overall distribution of primes.
The Zhang-Maynard-Tao Theorem
In recent years, significant breakthroughs have been made regarding gaps between primes. The Zhang-Maynard-Tao theorem proved the existence of infinitely many pairs of primes with a bounded gap, although the bound was initially quite large. Subsequent work has refined this bound, bringing us closer to proving the Twin Prime Conjecture. However, proving the conjecture remains a major open problem in number theory.
Twin Primes and Computational Approaches
The search for twin primes and the investigation of their properties are not solely theoretical pursuits. Computational methods play a vital role in exploring this area. Sophisticated algorithms and powerful computers are employed to identify extremely large twin prime pairs, contributing valuable data for ongoing research. These computational approaches can also help refine existing heuristics and inspire new conjectures.
Conclusion: The Enduring Enigma of Twin Primes
The study of twin primes from 1 to 100, while seemingly simple at first glance, provides a gateway into a profound and complex area of mathematics. The eight pairs found within this range, (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), and (71, 73), serve as a microcosm of the larger questions surrounding the distribution and infinitude of twin primes. While the Twin Prime Conjecture remains unproven, the ongoing research and advancements in number theory continuously bring us closer to understanding these fascinating number pairs and their intricate place within the vast landscape of mathematics. The seemingly simple question of whether there are infinitely many twin primes fuels ongoing research and continues to challenge mathematicians, highlighting the enduring allure of this fundamental mathematical problem. The quest to unravel the mysteries of twin primes remains a captivating journey of discovery.
Latest Posts
Latest Posts
-
What Is The Purpose Of Mitosis In Single Celled Organisms
Mar 31, 2025
-
What Is The Difference Between A Land And Sea Breeze
Mar 31, 2025
-
A Real Gas Behaves Most Like An Ideal Gas At
Mar 31, 2025
-
How Many Valence Electrons Are Found In Phosphorus
Mar 31, 2025
-
Write The Prime Factorization Of 21
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Twin Primes From 1 To 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
