Moment Of Inertia Of A Rectangular Plate
Juapaving
Mar 29, 2025 · 6 min read
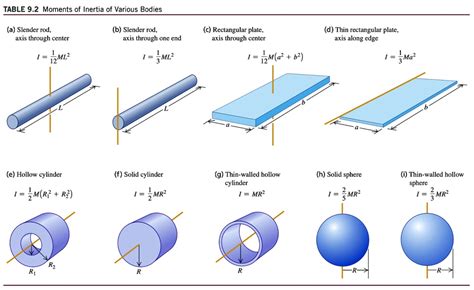
Table of Contents
Moment of Inertia of a Rectangular Plate: A Comprehensive Guide
The moment of inertia, a crucial concept in physics and engineering, quantifies an object's resistance to changes in its rotation. Understanding the moment of inertia is vital for analyzing the dynamics of rotating bodies, from simple pendulums to complex machinery. This comprehensive guide delves into the calculation of the moment of inertia for a rectangular plate, exploring various scenarios and providing practical applications.
Understanding Moment of Inertia
Before we dive into the specifics of a rectangular plate, let's solidify our understanding of the fundamental concept. The moment of inertia (often denoted as I) is analogous to mass in linear motion. While mass resists changes in linear velocity, the moment of inertia resists changes in angular velocity. A higher moment of inertia indicates a greater resistance to rotational acceleration.
The moment of inertia depends on:
- Mass: A more massive object naturally resists changes in rotation more strongly.
- Mass Distribution: How the mass is distributed relative to the axis of rotation significantly impacts the moment of inertia. Mass concentrated further from the axis contributes more significantly than mass closer to the axis.
- Axis of Rotation: The chosen axis of rotation is paramount. The moment of inertia will differ depending on whether the axis is through the center of mass, along an edge, or at some other point.
Calculating the Moment of Inertia of a Rectangular Plate
Calculating the moment of inertia of a rectangular plate involves integrating over the entire area of the plate. The general formula is:
I = ∫ r² dm
Where:
- I is the moment of inertia.
- r is the perpendicular distance from an infinitesimal mass element (dm) to the axis of rotation.
- dm is an infinitesimal mass element.
This integration can be simplified for a rectangular plate by considering its uniform mass density (ρ) and its dimensions (length 'a' and width 'b'). We'll explore different scenarios based on the axis of rotation.
1. Moment of Inertia about an Axis through the Center of Mass and Parallel to a Side
Let's consider a rectangular plate with mass M, length a, and width b. We'll calculate the moment of inertia (I<sub>x</sub>) about an axis passing through the center of mass and parallel to the side of length b.
We can express dm as:
dm = ρ dA = ρ dx dy
where ρ = M/(ab) is the mass density, and dA is an infinitesimal area element. The distance r from an element dm to the axis is simply x. The integral becomes:
I<sub>x</sub> = ∫∫ x² ρ dx dy
The limits of integration are from -a/2 to a/2 for x and -b/2 to b/2 for y. Solving this double integral yields:
I<sub>x</sub> = (1/12)Mb²
Similarly, the moment of inertia (I<sub>y</sub>) about an axis passing through the center of mass and parallel to the side of length a is:
I<sub>y</sub> = (1/12)Ma²
2. Moment of Inertia about an Axis through the Center of Mass and Perpendicular to the Plane
For an axis perpendicular to the plane of the rectangular plate and passing through its center of mass, the moment of inertia (I<sub>z</sub>) is simply the sum of I<sub>x</sub> and I<sub>y</sub>:
I<sub>z</sub> = I<sub>x</sub> + I<sub>y</sub> = (1/12)M(a² + b²)
This is known as the perpendicular axis theorem.
3. Moment of Inertia about an Axis through a Corner
Calculating the moment of inertia about an axis through a corner requires a different approach. Let's consider an axis through one corner and parallel to a side. Using the parallel axis theorem, we can relate the moment of inertia about an axis through the corner (I<sub>corner</sub>) to the moment of inertia about a parallel axis through the center of mass (I<sub>cm</sub>).
The parallel axis theorem states:
I<sub>corner</sub> = I<sub>cm</sub> + Md²
Where:
- I<sub>corner</sub> is the moment of inertia about the axis through the corner.
- I<sub>cm</sub> is the moment of inertia about the parallel axis through the center of mass.
- M is the mass of the rectangular plate.
- d is the distance between the two parallel axes.
For an axis through a corner and parallel to a side of length b, I<sub>cm</sub> = (1/12)Mb² and d² = (a²/4 + b²/4). Substituting these values, we get:
I<sub>corner</sub> = (1/12)Mb² + M((a²/4) + (b²/4)) = (1/3)M(a² + b²)
Similarly, for an axis through a corner and parallel to the side of length a, the moment of inertia would be:
I<sub>corner</sub> = (1/3)M(a² + b²)
Applications of Moment of Inertia of a Rectangular Plate
The moment of inertia of a rectangular plate finds applications in various engineering and physics domains:
-
Structural Engineering: Designing beams, plates, and other structural elements requires considering their resistance to bending and deflection under load. The moment of inertia plays a critical role in these calculations. A higher moment of inertia signifies greater stiffness and resistance to bending.
-
Mechanical Engineering: The design of rotating machinery, such as gears, flywheels, and rotors, necessitates careful consideration of the moment of inertia. The moment of inertia determines the rotational kinetic energy and affects the machine's dynamic behavior.
-
Robotics: The moment of inertia of robotic links and components influences the robot's motion and control. Accurate calculation of moment of inertia is crucial for effective robot design and control algorithms.
-
Aerospace Engineering: In aerospace design, the moment of inertia is vital for analyzing the stability and maneuverability of aircraft and spacecraft. The distribution of mass within the structure directly impacts its rotational dynamics.
Beyond the Basics: More Complex Scenarios
While we've covered the fundamental cases, more complex scenarios can arise:
-
Non-uniform Mass Density: If the rectangular plate doesn't have a uniform mass density, the integration becomes more challenging, requiring a more detailed description of the density function.
-
Composite Plates: When dealing with plates composed of different materials with varying densities, the calculation becomes more involved, requiring separate calculations for each component and then summing them up.
-
Plates with Cutouts: Plates with holes or cutouts require more sophisticated techniques, often involving superposition or numerical methods.
Conclusion
Calculating the moment of inertia of a rectangular plate is a fundamental problem in mechanics. Understanding the different formulas based on the axis of rotation and applying the parallel axis theorem is crucial for various engineering applications. While simple cases can be solved analytically, more complex scenarios may necessitate numerical techniques. This guide provided a comprehensive overview, equipping you with the knowledge to tackle a wide range of problems involving the rotational dynamics of rectangular plates. Remember, mastery of this concept is key to understanding and designing many physical systems. This deep understanding paves the way for more advanced studies in dynamics and control systems.
Latest Posts
Latest Posts
-
A Rectangle Is Sometimes A Square
Mar 31, 2025
-
The Two Purines In Dna Are
Mar 31, 2025
-
A To Z In Cursive Writing
Mar 31, 2025
-
What Is The Purpose Of Mitosis In Single Celled Organisms
Mar 31, 2025
-
What Is The Difference Between A Land And Sea Breeze
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Moment Of Inertia Of A Rectangular Plate . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
