Common Multiples Of 7 And 3
Juapaving
Mar 27, 2025 · 6 min read
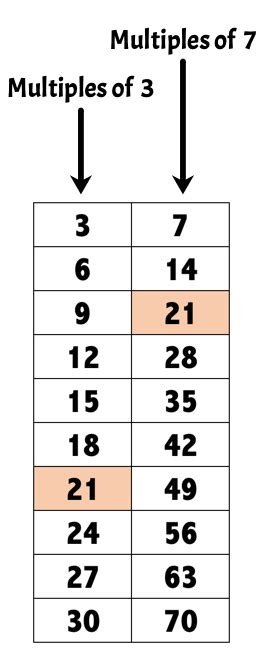
Table of Contents
Common Multiples of 7 and 3: A Deep Dive into Number Theory
Finding common multiples, especially for seemingly simple numbers like 7 and 3, opens a fascinating window into the world of number theory. While the concept might seem elementary at first glance, a deeper exploration reveals intricate patterns, elegant mathematical relationships, and practical applications across various fields. This comprehensive guide will delve into the common multiples of 7 and 3, exploring their properties, methods for finding them, and their significance in broader mathematical contexts.
Understanding Multiples and Common Multiples
Before we embark on our journey into the specifics of 7 and 3, let's solidify our understanding of fundamental concepts.
What is a Multiple?
A multiple of a number is the product of that number and any integer (whole number). For example, multiples of 7 include 7 (7 x 1), 14 (7 x 2), 21 (7 x 3), 28 (7 x 4), and so on. These extend infinitely in both positive and negative directions.
What is a Common Multiple?
A common multiple of two or more numbers is a number that is a multiple of each of those numbers. For instance, considering 7 and 3, a common multiple would be a number divisible by both 7 and 3.
Least Common Multiple (LCM)
Among the infinite set of common multiples, the least common multiple (LCM) holds special significance. It is the smallest positive common multiple of the given numbers. The LCM of 7 and 3 will be the smallest positive integer divisible by both 7 and 3.
Finding Common Multiples of 7 and 3: Methods and Techniques
Several methods can be employed to identify common multiples of 7 and 3. Let's explore some of the most effective approaches:
1. Listing Multiples:
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of 7 and 3 separately, then identify the common numbers.
Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105... Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105...
By comparing the two lists, we readily observe that 21, 42, 63, 84, 105, and many more are common multiples. The Least Common Multiple (LCM) in this case is 21.
2. Prime Factorization:
This method is more efficient for larger numbers. We find the prime factorization of each number and then construct the LCM.
7 is a prime number, so its prime factorization is simply 7. 3 is a prime number, so its prime factorization is simply 3.
To find the LCM, we take the highest power of each prime factor present in the factorizations: The prime factors are 3 and 7. Therefore, the LCM is 3 x 7 = 21.
3. Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD of 7 and 3 is 1 (as they share no common factors other than 1).
Therefore, LCM(7, 3) = (7 x 3) / 1 = 21
Significance and Applications of Common Multiples
The concept of common multiples, and specifically the LCM, extends far beyond simple mathematical exercises. It finds practical application in diverse fields:
1. Scheduling and Timing:
Imagine two buses arrive at a stop, one every 7 minutes and the other every 3 minutes. The LCM (21 minutes) determines when both buses will arrive simultaneously again. This principle is applicable in various scheduling problems, from traffic light synchronization to production line management.
2. Fraction Arithmetic:
Finding a common denominator when adding or subtracting fractions requires finding a common multiple of the denominators. For example, adding 1/7 and 1/3 requires finding a common denominator, which is the LCM of 7 and 3 (21). This allows us to rewrite the fractions as 3/21 and 7/21, facilitating addition.
3. Modular Arithmetic and Cryptography:
Common multiples play a crucial role in modular arithmetic, a branch of number theory used extensively in cryptography. The concept of congruence modulo n relies heavily on understanding multiples and their relationships.
4. Music Theory:
In music, the concept of harmony and consonance is related to the frequency ratios of musical notes. Common multiples can help determine when notes will sound harmonious together, creating pleasing musical intervals.
5. Geometry and Tessellations:
When arranging tiles or shapes to cover a plane without gaps or overlaps (tessellation), understanding common multiples helps determine the dimensions and arrangements needed for a successful tessellation. For example, creating a tessellation with two types of tiles, one 7 units long and the other 3 units wide, requires an understanding of their common multiples to ensure a seamless pattern.
Exploring Patterns and Relationships: Beyond the Basics
While finding the LCM of 7 and 3 is relatively straightforward, investigating the properties of their common multiples reveals deeper patterns and relationships:
-
Infinite Set: The set of common multiples of 7 and 3 is infinite. Once we find the LCM (21), any multiple of the LCM is also a common multiple. This means 42 (21 x 2), 63 (21 x 3), 84 (21 x 4), and so on are all common multiples.
-
Arithmetic Progression: The common multiples of 7 and 3 form an arithmetic progression with a common difference equal to the LCM (21). This means the sequence of common multiples can be expressed as: 21, 42, 63, 84, ... Each term is obtained by adding 21 to the previous term.
-
Divisibility Rules: Any number that is a common multiple of 7 and 3 must be divisible by both 7 and 3. This means it must satisfy the divisibility rules for both numbers. For instance, a number divisible by 3 has a sum of digits divisible by 3. A number divisible by 7 requires a slightly more complex test, but both rules must be satisfied for a number to be a common multiple.
-
Relationship to GCD: The product of two numbers is always equal to the product of their LCM and GCD. In the case of 7 and 3, (7 x 3) = (21 x 1), demonstrating this relationship.
Conclusion: The Enduring Importance of Common Multiples
The seemingly simple task of finding common multiples of 7 and 3 unveils a rich tapestry of mathematical concepts and practical applications. From scheduling problems to advanced cryptographic techniques, the understanding of common multiples and the LCM proves invaluable across various disciplines. This exploration highlights the beauty and elegance of number theory, showcasing how fundamental mathematical principles underpin complex systems and real-world challenges. The journey of uncovering the common multiples of 7 and 3 serves as a microcosm of the broader mathematical landscape, demonstrating the interconnectedness of seemingly disparate concepts and the enduring relevance of fundamental mathematical principles. Further exploration into number theory and its applications will reveal even deeper insights into the intricate patterns and relationships that govern the world of numbers.
Latest Posts
Latest Posts
-
In An Endothermic Reaction Energy Is
Mar 30, 2025
-
The Numerical Ratio Of Average Velocity To Average Speed Is
Mar 30, 2025
-
Which Of The Following Is A Vector
Mar 30, 2025
-
What Was Darwin Influences On Malthus
Mar 30, 2025
-
Is 6 A Factor Of 12
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Common Multiples Of 7 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
