Which Of The Following Is A Vector
Juapaving
Mar 30, 2025 · 5 min read
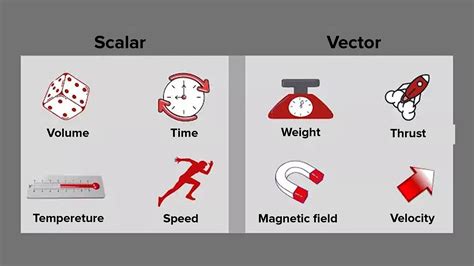
Table of Contents
Which of the Following is a Vector? Understanding Vectors and Scalars in Physics and Mathematics
Understanding the difference between vectors and scalars is fundamental to many fields, particularly physics and mathematics. While both represent quantities, they differ significantly in how they're described and used. This comprehensive guide will delve into the core concepts of vectors and scalars, providing clear explanations, examples, and practical applications to help you confidently identify which quantities are vectors.
What is a Scalar?
A scalar is a quantity that is fully described by its magnitude (size or amount). It simply tells you "how much" of something there is. Scalars are typically represented by a single number and a unit.
Examples of Scalars:
- Mass: 5 kg (kilograms)
- Temperature: 25 °C (degrees Celsius)
- Speed: 60 km/h (kilometers per hour) Note: Speed is a scalar, while velocity is a vector (explained below).
- Energy: 100 Joules (J)
- Time: 2 hours
- Volume: 10 liters
- Density: 1 g/cm³ (grams per cubic centimeter)
The key characteristic of a scalar is its simplicity. You don't need to consider direction; the magnitude alone completely defines it.
What is a Vector?
A vector, in contrast, is a quantity that possesses both magnitude and direction. This means you need to specify both "how much" and "which way." Vectors are often represented graphically as arrows, where the length of the arrow represents the magnitude and the arrow's direction indicates its direction.
Examples of Vectors:
- Displacement: 10 meters east (magnitude: 10 meters, direction: east)
- Velocity: 20 m/s north (magnitude: 20 m/s, direction: north)
- Force: 50 Newtons upwards (magnitude: 50 N, direction: upwards)
- Acceleration: 9.8 m/s² downwards (magnitude: 9.8 m/s², direction: downwards)
- Momentum: A moving object's mass multiplied by its velocity (both magnitude and direction are crucial).
- Electric Field: Describes the force per unit charge at a point in space, possessing both magnitude and direction.
- Magnetic Field: Similar to electric fields, magnetic fields have both magnitude and direction.
Key Differences Between Scalars and Vectors
| Feature | Scalar | Vector |
|---|---|---|
| Definition | Magnitude only | Magnitude and direction |
| Representation | Single number and unit | Arrow (length = magnitude, direction = arrow's direction) |
| Addition | Simple arithmetic addition | Requires vector addition (e.g., head-to-tail method, parallelogram method) |
| Multiplication | Simple multiplication | Scalar multiplication (changes magnitude), vector multiplication (dot product and cross product yield scalars and vectors respectively) |
| Examples | Mass, speed, temperature, energy | Displacement, velocity, force, acceleration |
Mathematical Representation of Vectors
Vectors are often represented mathematically using different notations:
- Boldface notation: v (where v is the vector)
- Arrow notation: →v
- Component notation: (v<sub>x</sub>, v<sub>y</sub>, v<sub>z</sub>) This represents a vector in three-dimensional space, where v<sub>x</sub>, v<sub>y</sub>, and v<sub>z</sub> are the components of the vector along the x, y, and z axes, respectively.
Vector Addition and Subtraction
Adding or subtracting vectors isn't as straightforward as adding scalars. You can't simply add their magnitudes. Instead, you must consider their directions. Common methods include:
- Head-to-tail method: Place the tail of the second vector at the head of the first vector. The resultant vector is drawn from the tail of the first vector to the head of the second vector.
- Parallelogram method: Draw the vectors from a common point. Complete the parallelogram. The resultant vector is the diagonal of the parallelogram starting from the common point.
Vector subtraction is essentially adding the negative of the vector being subtracted. The negative of a vector has the same magnitude but the opposite direction.
Vector Multiplication
There are two main types of vector multiplication:
-
Dot product (scalar product): This operation results in a scalar value. It's calculated as the product of the magnitudes of the two vectors and the cosine of the angle between them. It's useful for determining the work done by a force.
-
Cross product (vector product): This operation results in a vector that is perpendicular to both of the original vectors. Its magnitude is the product of the magnitudes of the two vectors and the sine of the angle between them. It's crucial in areas like torque calculations and magnetism.
Applications of Vectors
Vectors are essential tools in numerous scientific and engineering disciplines:
- Physics: Describing motion (velocity, acceleration), forces, fields (electric, magnetic, gravitational), and momentum.
- Engineering: Analyzing structural forces, designing aircraft and spacecraft, calculating fluid flow, and many other applications.
- Computer graphics: Representing positions, directions, and transformations of objects in 3D space.
- Computer science: Representing data in multi-dimensional spaces, implementing algorithms in machine learning.
- Meteorology: Describing wind speed and direction.
- Navigation: Calculating displacement, velocity, and course corrections.
Identifying Vectors: A Practical Approach
When determining whether a quantity is a vector, ask yourself these two questions:
- Does it have magnitude? If not, it's not a vector.
- Does it have direction? If it has both magnitude and direction, it is a vector.
Let's revisit some examples:
- Speed (scalar): A car travels at 60 km/h. This tells us the magnitude (60 km/h), but not the direction.
- Velocity (vector): A car travels at 60 km/h due north. This provides both magnitude (60 km/h) and direction (north).
- Distance (scalar): The total distance travelled is 100 km. Only magnitude is given.
- Displacement (vector): The displacement from the starting point is 50 km east. Both magnitude and direction are specified.
Conclusion
Distinguishing between vectors and scalars is crucial for understanding and applying many physical concepts and mathematical operations. By grasping the fundamental differences in their definitions, representations, and mathematical manipulations, you can confidently identify vectors and use them effectively in various contexts. Remember the key: vectors possess both magnitude and direction, while scalars possess only magnitude. This simple distinction is the foundation for understanding many complex phenomena in the world around us. Understanding vector calculus opens doors to more advanced topics in physics and mathematics, enhancing your ability to model and solve complex problems. So, keep practicing and exploring!
Latest Posts
Latest Posts
-
Find The Inverse Of The Relation
Apr 01, 2025
-
How Are Cellular Respiration And Photosynthesis Related
Apr 01, 2025
-
How Many Rna Polymerases Are Found In Prokaryotes
Apr 01, 2025
-
When Two Parallel Lines Are Crossed By A Transversal
Apr 01, 2025
-
Device That Converts Light Energy Into Electrical Energy
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Which Of The Following Is A Vector . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
