When Two Parallel Lines Are Crossed By A Transversal
Juapaving
Apr 01, 2025 · 7 min read
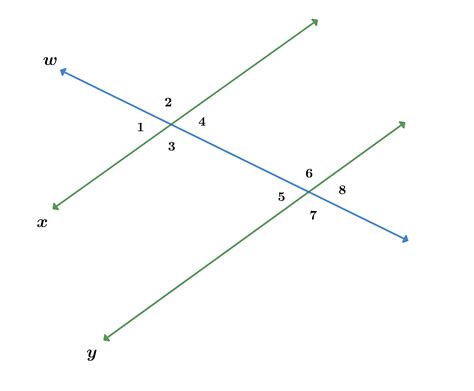
Table of Contents
When Two Parallel Lines are Crossed by a Transversal: A Comprehensive Guide
When two parallel lines are intersected by a transversal, a fascinating array of geometric relationships emerge. Understanding these relationships is fundamental to geometry, offering a cornerstone for more advanced mathematical concepts. This comprehensive guide will explore these relationships in detail, providing clear explanations, diagrams, and practical applications. We'll delve into the angles formed, their classifications, and the theorems that govern their interactions. By the end, you'll possess a solid understanding of this crucial geometric concept.
Understanding Parallel Lines and Transversals
Before diving into the specifics, let's define our key terms:
-
Parallel Lines: Two lines are parallel if they lie in the same plane and never intersect, regardless of how far they are extended. We often denote parallel lines using symbols like ||. For example, line l || line m.
-
Transversal: A transversal is a line that intersects two or more other lines at distinct points. It's crucial that the transversal intersects the lines at separate points to create the angles we'll be examining.
The Angles Formed: A Detailed Breakdown
When a transversal intersects two parallel lines, eight angles are created. These angles are categorized into several types based on their relative positions:
1. Corresponding Angles
Corresponding angles are pairs of angles that are in the same relative position at each intersection. They are located on the same side of the transversal and on the same side of the parallel lines.
(Image would be inserted here showing two parallel lines intersected by a transversal with corresponding angles clearly labeled)
- Theorem: If two parallel lines are cut by a transversal, then corresponding angles are congruent (equal).
Example: Angles 1 and 5, angles 2 and 6, angles 3 and 7, and angles 4 and 8 are corresponding angles. If line l || line m, then ∠1 ≅ ∠5, ∠2 ≅ ∠6, ∠3 ≅ ∠7, and ∠4 ≅ ∠8.
2. Alternate Interior Angles
Alternate interior angles are pairs of angles that are located between the parallel lines, on opposite sides of the transversal.
(Image would be inserted here showing two parallel lines intersected by a transversal with alternate interior angles clearly labeled)
- Theorem: If two parallel lines are cut by a transversal, then alternate interior angles are congruent.
Example: Angles 3 and 6, and angles 4 and 5 are alternate interior angles. If line l || line m, then ∠3 ≅ ∠6 and ∠4 ≅ ∠5.
3. Alternate Exterior Angles
Alternate exterior angles are pairs of angles that are located outside the parallel lines, on opposite sides of the transversal.
(Image would be inserted here showing two parallel lines intersected by a transversal with alternate exterior angles clearly labeled)
- Theorem: If two parallel lines are cut by a transversal, then alternate exterior angles are congruent.
Example: Angles 1 and 8, and angles 2 and 7 are alternate exterior angles. If line l || line m, then ∠1 ≅ ∠8 and ∠2 ≅ ∠7.
4. Consecutive Interior Angles (Same-Side Interior Angles)
Consecutive interior angles (also called same-side interior angles) are pairs of angles that are located between the parallel lines and on the same side of the transversal.
(Image would be inserted here showing two parallel lines intersected by a transversal with consecutive interior angles clearly labeled)
- Theorem: If two parallel lines are cut by a transversal, then consecutive interior angles are supplementary (their sum is 180°).
Example: Angles 3 and 5, and angles 4 and 6 are consecutive interior angles. If line l || line m, then ∠3 + ∠5 = 180° and ∠4 + ∠6 = 180°.
5. Consecutive Exterior Angles (Same-Side Exterior Angles)
Consecutive exterior angles (also called same-side exterior angles) are pairs of angles that are located outside the parallel lines and on the same side of the transversal.
(Image would be inserted here showing two parallel lines intersected by a transversal with consecutive exterior angles clearly labeled)
- Theorem: If two parallel lines are cut by a transversal, then consecutive exterior angles are supplementary.
Example: Angles 1 and 7, and angles 2 and 8 are consecutive exterior angles. If line l || line m, then ∠1 + ∠7 = 180° and ∠2 + ∠8 = 180°.
Proofs of the Theorems
The theorems stated above aren't just assertions; they can be rigorously proven using fundamental geometric principles. While a detailed proof for each would extend this guide significantly, the core logic typically involves demonstrating that the angles are either vertically opposite (hence congruent), or form a linear pair (hence supplementary). The parallelism of the lines is crucial to establishing these relationships.
Applications and Real-World Examples
The concepts of parallel lines and transversals aren't confined to the realm of theoretical geometry. They have numerous practical applications in various fields:
-
Architecture and Construction: Understanding angles and parallel lines is critical in designing stable and structurally sound buildings, bridges, and other structures. Parallel lines ensure walls are straight and evenly spaced, while the angles formed by transversals (like roof beams intersecting walls) are crucial for calculating load distribution and structural integrity.
-
Civil Engineering: Road design often utilizes parallel lines and transversals. The angles formed by intersecting roads are crucial for traffic flow and safety. Understanding these angles helps engineers plan efficient and safe road networks.
-
Computer Graphics and CAD: In computer-aided design (CAD) and computer graphics, parallel lines and transversals are used extensively to create precise 2D and 3D models. These concepts are fundamental to algorithms that manipulate shapes and lines within digital environments.
-
Cartography and Mapping: Parallel lines and transversals are used in creating maps and geographic projections. Understanding how lines intersect and relate to each other is crucial for accurate representation of geographical features.
-
Navigation: Concepts related to parallel lines and transversals can help in navigation. Determining the angle between two known directions can aid in setting courses and avoiding obstacles.
Solving Problems Involving Parallel Lines and Transversals
Many geometry problems involve determining the measure of angles when parallel lines are intersected by a transversal. Here’s a step-by-step approach:
-
Identify Parallel Lines and the Transversal: Clearly identify the lines that are parallel and the line that intersects them.
-
Classify the Angles: Determine the type of angles involved (corresponding, alternate interior, alternate exterior, consecutive interior, or consecutive exterior).
-
Apply the Appropriate Theorem: Use the relevant theorem to establish relationships between the angles. Remember that corresponding, alternate interior, and alternate exterior angles are congruent, while consecutive interior and consecutive exterior angles are supplementary.
-
Solve for the Unknown Angle: Use algebraic equations to solve for any unknown angles, leveraging the relationships you've identified.
Example Problem: Two parallel lines are intersected by a transversal. One of the alternate interior angles measures 70°. What are the measures of the other seven angles?
(Image would be inserted here showing the example problem with labeled angles)
Solution:
-
Since alternate interior angles are congruent, the other alternate interior angle also measures 70°.
-
Corresponding angles are congruent, so two other angles measure 70°.
-
Consecutive interior angles are supplementary, so two angles will measure 180° - 70° = 110°.
-
The remaining angles are either vertically opposite to angles we've already solved for or are alternate exterior angles corresponding to known angles. Therefore we can deduce their measurements.
Beyond the Basics: Exploring Extensions
The concepts discussed so far lay the groundwork for more advanced geometric concepts. Understanding the relationships between angles formed by parallel lines and transversals is crucial for tackling problems involving:
-
Triangles: Many triangle theorems and properties rely heavily on the relationships established by parallel lines and transversals.
-
Polygons: Extending these ideas to polygons allows us to determine angle sums, interior angles, and exterior angles.
-
Coordinate Geometry: Applying algebraic equations to lines and angles enables solving more complex problems and geometric proofs.
Conclusion
The intersection of two parallel lines by a transversal is a fundamental concept in geometry, with profound implications for various fields. By understanding the relationships between the angles formed – corresponding, alternate interior, alternate exterior, and consecutive interior/exterior angles – we can solve a wide array of geometric problems and appreciate the practical applications of this elegant mathematical concept. Mastering these concepts opens doors to more advanced geometric studies and strengthens analytical skills applicable across diverse disciplines. Continuous practice and problem-solving are key to solidifying your understanding and mastering this essential area of geometry.
Latest Posts
Latest Posts
-
How To Find The Complement Of An Angle
Apr 02, 2025
-
Nice Word That Starts With E
Apr 02, 2025
-
200 Inches Is How Many Feet
Apr 02, 2025
-
Is Boiling A Physical Or Chemical Change
Apr 02, 2025
-
Rectangle Has How Many Lines Of Symmetry
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about When Two Parallel Lines Are Crossed By A Transversal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
