What Is The Square Root Of 23
Juapaving
Mar 26, 2025 · 5 min read
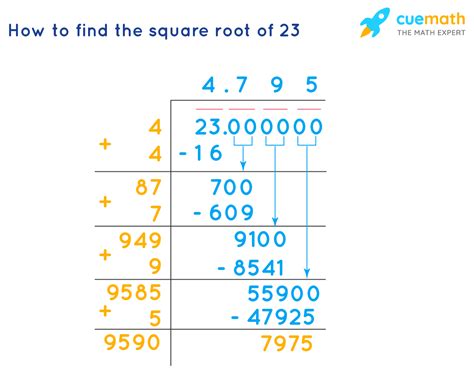
Table of Contents
What is the Square Root of 23? A Deep Dive into Irrational Numbers
The seemingly simple question, "What is the square root of 23?", opens a door to a fascinating world of mathematics, specifically the realm of irrational numbers. While a quick calculator search will give you a decimal approximation, understanding why the square root of 23 is what it is requires a deeper exploration of its properties and implications. This article will delve into the intricacies of this seemingly straightforward mathematical concept, covering its calculation, its significance in various fields, and its place within the broader landscape of number theory.
Understanding Square Roots
Before we tackle the specific case of the square root of 23, let's establish a foundational understanding of square roots. The square root of a number 'x' is a value that, when multiplied by itself, equals 'x'. In mathematical notation, this is represented as √x. For example:
- √9 = 3 because 3 * 3 = 9
- √16 = 4 because 4 * 4 = 16
- √25 = 5 because 5 * 5 = 25
These are all examples of perfect squares, numbers that have integer square roots. However, many numbers do not have integer square roots. This is where the concept of irrational numbers comes into play.
Irrational Numbers and the Square Root of 23
The square root of 23 is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation is non-terminating and non-repeating; it goes on forever without ever settling into a predictable pattern. This is a fundamental characteristic that distinguishes it from rational numbers like 1/2 or 0.75.
Calculating the Square Root of 23:
Calculating the exact value of √23 is impossible using simple arithmetic. Instead, we rely on approximation methods. These methods include:
-
Babylonian Method (or Heron's Method): This iterative method refines an initial guess to get progressively closer to the true value. It involves repeatedly averaging a number and its reciprocal to obtain a more accurate approximation.
-
Newton-Raphson Method: A more advanced iterative method that uses calculus to converge more rapidly towards the solution.
-
Calculators and Computers: Modern calculators and computers utilize sophisticated algorithms based on these and other methods to provide highly accurate decimal approximations.
Using a calculator, we find that the square root of 23 is approximately 4.79583152331. This is just an approximation; the true value has infinitely many decimal places.
The Significance of Irrational Numbers
The existence of irrational numbers, like the square root of 23, has profound implications in mathematics and beyond. They challenge the intuitive notion that all numbers can be neatly expressed as fractions. Their discovery, particularly that of the square root of 2 (which is also irrational), caused a significant crisis in ancient Greek mathematics.
The discovery highlighted the limitations of rational numbers in representing geometric quantities. For instance, the diagonal of a square with side length 1 has a length of √2, demonstrating that not all lengths can be expressed using rational numbers. This led to advancements in mathematical understanding and the development of more sophisticated number systems.
Applications of the Square Root of 23
While the square root of 23 might not be as prominently featured as some other irrational numbers (like π or e), it still finds applications in various fields:
-
Geometry and Trigonometry: The square root of 23 could appear in calculations involving triangles and other geometric shapes, especially when dealing with non-perfect squares.
-
Physics and Engineering: In physics and engineering applications, calculations involving distances, velocities, or forces might involve irrational numbers like √23.
-
Computer Graphics and Modeling: In computer simulations and three-dimensional modeling, irrational numbers are essential for accurate representation of shapes and objects.
-
Statistics and Probability: Irrational numbers can emerge in statistical analysis, particularly when dealing with distributions and probability calculations.
Approximating √23 Using the Babylonian Method
Let's illustrate the Babylonian method for approximating √23. We'll start with an initial guess of 5 (since 5*5 = 25, which is close to 23).
Iteration 1:
- Guess: 5
- Average of 5 and 23/5: (5 + 23/5) / 2 ≈ 4.8
Iteration 2:
- Guess: 4.8
- Average of 4.8 and 23/4.8: (4.8 + 23/4.8) / 2 ≈ 4.79583
Iteration 3:
- Guess: 4.79583
- Average of 4.79583 and 23/4.79583: (4.79583 + 23/4.79583) / 2 ≈ 4.79583152
As you can see, with each iteration, the approximation gets closer to the actual value of √23 provided by a calculator.
Comparing √23 to other Irrational Numbers
It's instructive to compare √23 to other well-known irrational numbers:
-
π (pi): Approximately 3.14159... The ratio of a circle's circumference to its diameter. This is a fundamental constant in geometry.
-
e (Euler's number): Approximately 2.71828... The base of the natural logarithm, crucial in calculus and exponential growth.
-
√2: Approximately 1.41421... The diagonal of a unit square. Historically significant for its role in the discovery of irrational numbers.
Unlike π and e, which are transcendental numbers (they are not the root of any polynomial equation with rational coefficients), √23 is an algebraic number (it is the root of the polynomial equation x² - 23 = 0).
Conclusion: The Enduring Mystery of √23
The square root of 23, while seemingly a simple mathematical concept, reveals the rich tapestry of number theory. Its irrationality highlights the limitations of representing all numbers using simple fractions. This seemingly simple number is involved in numerous scientific, engineering, and mathematical applications, demonstrating the importance of understanding irrational numbers and their properties. While we can approximate its value to a high degree of accuracy, the true value of √23 remains an unending, fascinating exploration into the world of mathematics. The continued investigation and understanding of irrational numbers like √23 continues to drive advancements in various fields, highlighting the enduring mystery and beauty of mathematics.
Latest Posts
Latest Posts
-
What Is The Lcm Of 14 And 12
Mar 29, 2025
-
Find The Greatest Common Factor Of 12 And 18
Mar 29, 2025
-
Which Graph Represents An Odd Function
Mar 29, 2025
-
How Is A Rhombus Similar To A Square
Mar 29, 2025
-
Is The Equation For Molarity Applicable To A Phsyical Experiment
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 23 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
