Is The Equation For Molarity Applicable To A Phsyical Experiment
Juapaving
Mar 29, 2025 · 5 min read
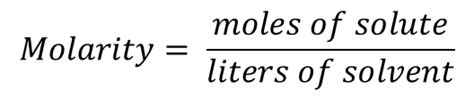
Table of Contents
Is the Equation for Molarity Applicable to a Physical Experiment?
The equation for molarity, a fundamental concept in chemistry, is deceptively simple: Molarity (M) = moles of solute / liters of solution. While seemingly straightforward, its applicability to a physical experiment requires a nuanced understanding of its limitations and the practical considerations involved in its accurate determination. This article delves into the nuances of using the molarity equation in a physical experiment, exploring its theoretical underpinnings, practical challenges, and the critical factors influencing its accuracy.
Understanding the Theoretical Foundation
The molarity equation rests on the premise of a homogeneous solution, where the solute is uniformly distributed throughout the solvent. This ideal scenario rarely translates perfectly to real-world experiments. Several factors can contribute to deviations from this ideal:
1. Incomplete Dissolution:
A key assumption is that the solute completely dissolves in the solvent. However, many substances exhibit limited solubility, meaning only a portion dissolves, leaving undissolved solute at the bottom of the container. In such cases, the measured mass of solute might not accurately reflect the amount actually contributing to the solution's molarity. This is particularly relevant for sparingly soluble salts or poorly soluble organic compounds. Careful experimental techniques, including stirring, heating (if appropriate), and sufficient time for dissolution, are essential to minimize this error.
2. Temperature Effects:
Molarity, as defined, is temperature-dependent. As temperature changes, the volume of the solution can expand or contract, directly affecting the denominator of the equation. Furthermore, the solubility of many substances is also temperature-dependent. An increase in temperature often increases solubility, leading to a higher concentration than initially calculated if the solution was prepared at a lower temperature. Maintaining a constant temperature throughout the experiment is crucial for accurate molarity determination. Using temperature-controlled baths or meticulously recording temperature fluctuations are key experimental measures.
3. Volume Changes Upon Mixing:
When mixing two or more solutions, the final volume isn't always the simple sum of the individual volumes. This phenomenon is known as volume contraction or expansion. This deviation stems from intermolecular interactions between solute and solvent molecules. For example, when mixing ethanol and water, a slight volume contraction occurs. This means the final volume will be slightly less than the sum of the initial volumes, leading to an overestimation of the final molarity if the simple additive approach is used.
4. Solution Non-Ideality:
The molarity equation assumes the solution behaves ideally; however, real solutions often deviate from ideality. Deviations arise due to intermolecular interactions between solute and solvent molecules. Strong intermolecular forces can lead to significant deviations from ideal behavior, especially at higher concentrations. These deviations are often accounted for using activity coefficients, which correct for non-ideal behavior, but this introduces additional complexity to the calculations.
Practical Challenges and Error Minimization
Applying the molarity equation accurately in a physical experiment hinges on minimizing experimental errors. Several aspects warrant careful consideration:
1. Accurate Weighing:
Precise measurement of the solute's mass is fundamental. Using an analytical balance with appropriate calibration and handling procedures is paramount to reduce weighing errors. Careful recording of the solute's mass and considering significant figures are essential for accurate molarity calculation.
2. Precise Volume Measurement:
Volumetric glassware, such as volumetric flasks and pipettes, plays a crucial role in ensuring accurate volume measurements. Using appropriately sized and calibrated glassware is essential. Understanding the tolerances of the glassware used and adhering to proper techniques for filling and reading the meniscus minimizes volumetric errors.
3. Proper Mixing:
Thorough mixing of the solution is crucial to achieve homogeneity. Incomplete mixing can lead to concentration gradients, rendering the molarity calculation inaccurate. Employing appropriate mixing techniques, such as swirling or magnetic stirring, is crucial. The duration of mixing should be sufficient to ensure homogeneity.
4. Calibration and Maintenance of Equipment:
The accuracy of molarity measurements depends heavily on the calibration and proper maintenance of the equipment used. Regular calibration of balances and volumetric glassware is essential to ensure accurate measurements. Keeping meticulous records of calibrations and any maintenance performed on the equipment is crucial for traceability and reliability of the results.
5. Contamination:
Contamination of the solute or the solvent can introduce significant errors. Using clean and dry glassware and ensuring the purity of the chemicals used are vital. Implementing proper cleaning procedures and handling techniques minimizes the risk of contamination.
Advanced Considerations: Activity and Ionic Strength
For ionic solutions, the concept of activity replaces concentration in more rigorous calculations. Activity accounts for the non-ideal behavior of ions in solution due to interionic interactions. The activity coefficient, γ, corrects for these deviations:
a = γ * c, where 'a' is the activity, 'γ' is the activity coefficient, and 'c' is the concentration (molarity).
The activity coefficient is influenced by the ionic strength (I) of the solution, defined as:
I = 1/2 Σ mi zi², where 'mi' is the molality of ion 'i' and 'zi' is its charge.
Calculating the activity coefficient often involves employing empirical equations like the Debye-Hückel equation, which considers the ionic strength and other factors. For dilute solutions, the activity coefficient approaches unity (γ ≈ 1), and the molarity approximates the activity. However, for concentrated solutions, the deviations become significant, necessitating the use of activity coefficients for accurate calculations.
Conclusion: Applicability and Limitations
The molarity equation serves as a cornerstone in chemical calculations, but its applicability to a physical experiment necessitates a critical assessment of potential errors and deviations from ideality. While the equation provides a useful approximation, achieving accurate molarity determinations requires meticulous experimental design, rigorous techniques, and an awareness of the limitations imposed by factors like incomplete dissolution, temperature variations, volume changes upon mixing, and solution non-ideality. For ionic solutions, the use of activity coefficients becomes essential for accurate representation of the effective concentration. By carefully considering these factors and employing appropriate error minimization strategies, researchers can leverage the molarity equation effectively to obtain reliable and meaningful results in physical experiments. The pursuit of accuracy demands careful attention to detail and a thorough understanding of the underlying principles governing solution chemistry. This conscientious approach ensures the validity and reliability of experimental findings.
Latest Posts
Latest Posts
-
Is Oxygen A Metal Nonmetal Or Metalloid
Mar 31, 2025
-
Keyboard Is A Hardware Or Software
Mar 31, 2025
-
Is 45 A Multiple Of 9
Mar 31, 2025
-
Forward Primer And Reverse Primer In Pcr
Mar 31, 2025
-
Words That Begin With A H
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Is The Equation For Molarity Applicable To A Phsyical Experiment . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
