Which Graph Represents An Odd Function
Juapaving
Mar 29, 2025 · 6 min read
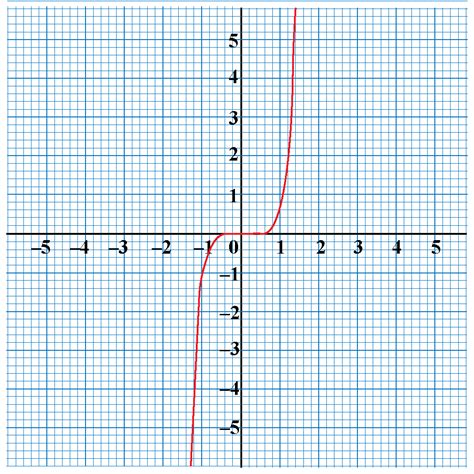
Table of Contents
Which Graph Represents an Odd Function? A Comprehensive Guide
Understanding function types is crucial in mathematics, particularly when dealing with graphs and their properties. This comprehensive guide delves into the characteristics of odd functions and how to identify them visually through their graphical representations. We will explore the definition of odd functions, their key properties, and provide numerous examples to solidify your understanding. By the end, you'll be able to confidently identify an odd function from its graph.
Defining Odd Functions: The Mathematical Perspective
Before we jump into graphical representations, let's solidify our understanding of the mathematical definition of an odd function. A function, f(x), is considered odd if it satisfies the following condition:
f(-x) = -f(x) for all x in the domain.
This means that if you replace x with -x, the output of the function will be the negative of the original output. This symmetry is the key to visually identifying odd functions on a graph.
Visual Identification: Key Characteristics of Odd Function Graphs
The defining characteristic of an odd function's graph is its origin symmetry. This means the graph is symmetric about the origin (0,0). Imagine folding the graph along the x-axis and then folding it again along the y-axis. If the graph perfectly overlaps itself, then it represents an odd function.
Here's a breakdown of how this origin symmetry manifests:
-
Symmetry across the origin: If a point (a, b) lies on the graph of an odd function, then the point (-a, -b) must also lie on the graph. This implies that for every point on one side of the origin, there's a corresponding point directly opposite it on the other side.
-
Rotational Symmetry: Another way to view this symmetry is through rotation. If you rotate the graph of an odd function 180 degrees about the origin, the graph will remain unchanged. This rotational symmetry is equivalent to the origin symmetry.
-
Absence of y-intercept (except at the origin): Unless the function is identically zero (f(x) = 0 for all x), an odd function will not have a y-intercept except at the origin (0,0). This is because if it had a y-intercept at (0, c) where c ≠ 0, the point (0, -c) would also need to be on the graph, violating the single-valued nature of a function.
Examples of Odd Functions and Their Graphs
Let's examine some common odd functions and their graphical representations to reinforce our understanding:
1. The Identity Function: f(x) = x
This is the simplest example of an odd function. Its graph is a straight line passing through the origin with a slope of 1. Clearly, f(-x) = -x = -f(x), satisfying the definition. The graph displays perfect origin symmetry.
2. Cubic Function: f(x) = x³
The graph of f(x) = x³ is also symmetric about the origin. Observe that f(-x) = (-x)³ = -x³ = -f(x). The graph increases monotonically, but maintains the origin symmetry crucial for odd functions.
3. f(x) = x⁵
Similarly, higher odd-powered functions like f(x) = x⁵ maintain origin symmetry. The graph will resemble the cubic function but with a steeper increase and sharper curve. Again, f(-x) = (-x)⁵ = -x⁵ = -f(x).
4. Sine Function: f(x) = sin(x)
The sine function is a classic example of an odd function. Its graph oscillates around the x-axis, exhibiting perfect origin symmetry. You can easily verify that sin(-x) = -sin(x). This is fundamental to many trigonometric identities and applications.
5. f(x) = x³ - x
This function combines a cubic and linear term, both odd functions. The sum or difference of odd functions will also be an odd function. If we plug in -x we obtain (-x)³ - (-x) = -x³ + x = -(x³ - x) = -f(x), fulfilling the odd function condition. The graph will show origin symmetry.
6. f(x) = x⁷ - 3x⁵ + x
This showcases that any polynomial function made solely from terms with odd powers is an odd function. Each term individually is odd, and their linear combinations remain odd.
Examples of Functions That Are NOT Odd
To fully grasp the concept of odd functions, it's equally important to understand what constitutes a non-odd function. These functions will lack origin symmetry. Let's explore some examples:
1. Even Functions: f(x) = x²
Even functions satisfy f(-x) = f(x). Their graphs are symmetric about the y-axis. The parabola of f(x) = x² is a classic example. It is clearly not symmetric about the origin.
2. Constant Functions: f(x) = c (where c is a constant)
A horizontal line representing a constant function has y-axis symmetry but not origin symmetry. It's neither odd nor even unless the constant is zero.
3. f(x) = x² + x
This function combines an even and an odd function. The resultant function is neither even nor odd. Observe that f(-x) = (-x)² + (-x) = x² - x ≠ f(x) and ≠ -f(x). The graph won’t exhibit origin symmetry.
4. Exponential Functions: f(x) = aˣ (where a > 0 and a ≠ 1)
Exponential functions typically do not possess any symmetry, therefore they are neither even nor odd.
Identifying Odd Functions from Graphs: A Practical Approach
When presented with a graph, follow these steps to determine if it represents an odd function:
-
Check for Origin Symmetry: The most straightforward approach is to visually inspect the graph for symmetry about the origin. Imagine folding the graph along both axes. If it perfectly overlaps itself, it's likely an odd function.
-
Test Key Points: Select several points on the graph. For each point (a, b), check if the point (-a, -b) also lies on the graph. If this holds true for several points, it strongly suggests the function is odd.
-
Consider the Function's Behavior: If the graph oscillates symmetrically about the origin (like the sine function) or exhibits a characteristic shape with origin symmetry (like a cubic function), it's a good indication that the function is odd.
Advanced Considerations: Piecewise Functions and Non-Elementary Functions
The concept of odd functions extends beyond simple polynomial and trigonometric functions. Let's briefly explore its application to more complex scenarios:
1. Piecewise Functions: A piecewise function might be odd if each piece individually adheres to the odd function condition and the entire function maintains origin symmetry. Careful analysis of each piece is necessary.
2. Non-Elementary Functions: Functions defined by integrals, infinite series, or other complex operations might still be odd. In these cases, proving oddness often requires applying the definition f(-x) = -f(x) directly.
Conclusion: Mastering the Identification of Odd Functions
Identifying odd functions from their graphs relies on understanding the concept of origin symmetry. By mastering the visual characteristics and applying the steps outlined in this guide, you'll develop the ability to quickly and accurately determine whether a given graph represents an odd function. Remember, the key lies in the relationship between points (a, b) and (-a, -b), and the consistent origin symmetry of the graphical representation. This understanding forms a crucial foundation for advanced mathematical concepts and applications.
Latest Posts
Latest Posts
-
The Preferred Energy Fuel For The Brain Is Fat
Mar 31, 2025
-
How Many Hours Is 1800 Minutes
Mar 31, 2025
-
In Glycolysis There Is A Net Gain Of Atp
Mar 31, 2025
-
The Clavicle Articulates With The Sternum And The Scapula
Mar 31, 2025
-
Is Oxygen A Metal Nonmetal Or Metalloid
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Which Graph Represents An Odd Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
