How Is A Rhombus Similar To A Square
Juapaving
Mar 29, 2025 · 5 min read
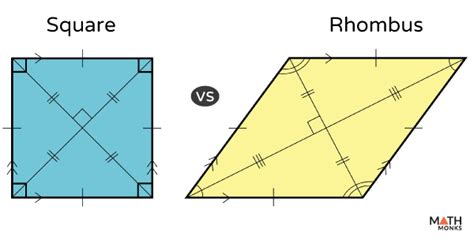
Table of Contents
How is a Rhombus Similar to a Square? Exploring Shared Properties and Key Differences
Squares and rhombuses, both belonging to the fascinating family of quadrilaterals, share a surprising number of similarities. While they are distinct shapes with unique characteristics, understanding their shared properties provides a deeper appreciation for the geometry of these fundamental figures. This article delves into the similarities between a rhombus and a square, highlighting their common features while also elucidating the crucial distinctions that set them apart.
Unveiling the Common Ground: Shared Properties of Rhombuses and Squares
At first glance, a square and a rhombus may seem quite different. However, a closer examination reveals a significant overlap in their properties. The most crucial commonality lies in their sides:
1. All Sides are Equal:
This is the cornerstone of their shared characteristics. Both a rhombus and a square possess four sides of equal length. This defining feature is fundamental to their classification and explains many of their other shared properties. This equal-sided characteristic immediately distinguishes them from other quadrilaterals like rectangles or parallelograms which may only have opposite sides equal.
2. Opposite Sides are Parallel:
This property flows directly from the equal side lengths and the definition of a parallelogram. Both rhombuses and squares are parallelograms, meaning their opposite sides are parallel to each other. This parallelism contributes to several other geometric relationships within the shapes.
3. Opposite Angles are Equal:
Another direct consequence of their parallelogram nature is the equality of opposite angles. In both rhombuses and squares, the opposite angles are congruent, meaning they have the same measure. This congruent angle property is essential when calculating areas, diagonals, and solving geometric problems involving these shapes.
Beyond the Basics: Deeper Similarities
While the above properties form the foundation of their similarity, a deeper dive reveals additional commonalities:
4. Diagonals Bisect Each Other:
Both rhombuses and squares have diagonals that bisect each other. This means each diagonal cuts the other into two equal segments. This property is crucial for various geometric constructions and calculations. The point of intersection of the diagonals is the center of the shape and can serve as a reference point for various measurements and analyses.
5. Diagonals Create Right Angles (in Squares, Always; in Rhombuses, Sometimes):
This is where a subtle but important difference emerges. In a square, the diagonals always intersect at right angles (90 degrees). This right angle intersection is a defining characteristic of a square. In a rhombus, however, the diagonals only intersect at right angles if, and only if, the rhombus is also a square. In other words, the right angle intersection of diagonals is a sufficient but not necessary condition for a rhombus to be a square.
6. Area Calculation Similarities:
The area calculation methods for both shapes share some similarity. While the formula itself might look different, the underlying principle relies on the length of their sides and/or diagonals. In a square, the area is simply the side length squared (side * side). For a rhombus, the area can be calculated using the formula (1/2) * d1 * d2, where d1 and d2 represent the lengths of the two diagonals. Note that this formula also applies to squares, but the diagonals of a square are equal in length.
The Distinguishing Feature: Angles
While they share numerous properties, the crucial difference between a rhombus and a square lies in their angles:
7. Angle Properties:
A square is defined by having four equal angles, each measuring 90 degrees. This characteristic makes it a special type of rhombus, a rectangle, and a parallelogram, all at once. In contrast, a rhombus only requires that opposite angles be equal; however, these angles do not need to measure 90 degrees. A rhombus can have any angle measure from slightly greater than 0 degrees to slightly less than 180 degrees. This variability in angle measurements is the defining difference between a rhombus and a square.
Summarizing the Similarities: A Table for Clarity
To better illustrate the shared properties, let's summarize them in a table:
| Property | Rhombus | Square |
|---|---|---|
| All Sides Equal | Yes | Yes |
| Opposite Sides Parallel | Yes | Yes |
| Opposite Angles Equal | Yes | Yes (90 degrees each) |
| Diagonals Bisect Each Other | Yes | Yes |
| Diagonals Perpendicular | Only if it's a square | Always |
| Four Equal Angles | No (except when it's a square) | Yes (90 degrees each) |
Exploring Applications: Real-World Examples
The properties of rhombuses and squares find applications in various fields:
Architecture and Design:
Squares and rhombuses are frequently used in architectural designs, tiling patterns, and building structures. The stability and symmetry provided by these shapes make them ideal for creating strong and aesthetically pleasing designs. Think of the diamond patterns in stained glass windows or the square tiles commonly used in flooring.
Engineering and Construction:
The predictable geometrical properties of these shapes are advantageous in engineering and construction. Their rigidity and predictable behavior under stress are crucial in building sturdy structures.
Art and Design:
Rhombuses and squares are often incorporated in artistic works and graphic design. Their geometric precision and visual appeal contribute to creating balanced and striking compositions. The versatility of their use in different contexts highlights their importance as fundamental geometric shapes.
Conclusion: Understanding the Subtle Differences
In conclusion, although rhombuses and squares share several significant properties – all sides equal, opposite sides parallel, opposite angles equal, and bisecting diagonals – the key distinction lies in their angles. Squares are a special type of rhombus with four 90-degree angles. Understanding these similarities and differences is crucial for anyone working with geometry, whether in academic pursuits, practical applications, or artistic endeavors. The shared properties highlight the underlying connections within the realm of geometry, illustrating how seemingly distinct shapes can possess deep-seated relationships. By appreciating these connections, we gain a richer and more nuanced understanding of the geometric world around us.
Latest Posts
Latest Posts
-
Is Oxygen A Metal Nonmetal Or Metalloid
Mar 31, 2025
-
Keyboard Is A Hardware Or Software
Mar 31, 2025
-
Is 45 A Multiple Of 9
Mar 31, 2025
-
Forward Primer And Reverse Primer In Pcr
Mar 31, 2025
-
Words That Begin With A H
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Is A Rhombus Similar To A Square . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
