What Is The Square Root 196
Juapaving
Mar 21, 2025 · 5 min read
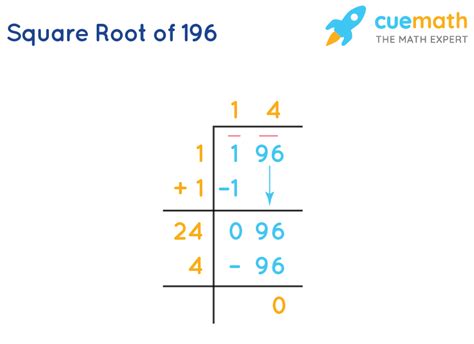
Table of Contents
- What Is The Square Root 196
- Table of Contents
- What is the Square Root of 196? A Deep Dive into Square Roots and Their Applications
- Understanding Square Roots: The Fundamentals
- Calculating the Square Root of 196: Methods and Approaches
- 1. Prime Factorization: A Systematic Approach
- 2. Mental Calculation for Perfect Squares: Recognizing Patterns
- 3. Using a Calculator: The Quickest Method
- Beyond the Calculation: Applications of Square Roots
- 1. Geometry and Measurement: Calculating Areas and Distances
- 2. Physics and Engineering: Understanding Motion and Forces
- 3. Statistics and Probability: Analyzing Data and Risk
- 4. Computer Graphics and Game Development: Creating Realistic Visuals
- 5. Finance and Investment: Calculating Returns and Risk
- Conclusion: The Square Root of 196 and Beyond
- Latest Posts
- Latest Posts
- Related Post
What is the Square Root of 196? A Deep Dive into Square Roots and Their Applications
The question, "What is the square root of 196?" might seem simple at first glance. A quick calculation reveals the answer: 14. But delving deeper, we uncover a wealth of mathematical concepts and practical applications that make understanding square roots far more enriching than a simple numerical answer. This article will explore the meaning of square roots, various methods for calculating them (including the square root of 196), and their relevance in diverse fields.
Understanding Square Roots: The Fundamentals
Before we tackle the square root of 196 specifically, let's establish a solid understanding of square roots in general. A square root of a number x is a value that, when multiplied by itself, equals x. In mathematical notation, this is represented as √x. Therefore, if a² = x, then a is the square root of x.
It's crucial to note that most numbers have two square roots: a positive and a negative one. For instance, the square roots of 25 are +5 and -5 because 5 x 5 = 25 and (-5) x (-5) = 25. However, when we talk about the square root, we generally refer to the principal square root, which is the non-negative square root. Therefore, √25 = 5.
Calculating the Square Root of 196: Methods and Approaches
Several methods exist for calculating square roots, ranging from simple mental math for perfect squares to more complex algorithms for non-perfect squares. Let's examine how we can determine that the square root of 196 is 14:
1. Prime Factorization: A Systematic Approach
Prime factorization involves breaking down a number into its prime factors – numbers divisible only by 1 and themselves. This method is particularly helpful for perfect squares.
- Factor 196: We can start by dividing 196 by 2 repeatedly: 196 = 2 x 98 = 2 x 2 x 49 = 2 x 2 x 7 x 7.
- Pair the factors: Notice that we have two 2s and two 7s. This indicates that 196 is a perfect square.
- Calculate the square root: Since we have pairs of factors, we take one factor from each pair and multiply them: 2 x 7 = 14. Therefore, √196 = 14.
This method provides a clear visual representation of why 196 is a perfect square and how its square root is derived.
2. Mental Calculation for Perfect Squares: Recognizing Patterns
With practice, recognizing perfect squares becomes easier. Knowing that 10² = 100 and 15² = 225, it's relatively straightforward to deduce that the square root of 196 lies somewhere between 10 and 15. A little more mental calculation quickly pinpoints 14 as the answer. This method is fast for numbers you frequently encounter.
3. Using a Calculator: The Quickest Method
For larger numbers or when speed is paramount, a calculator provides the most efficient way to find the square root. Simply input 196 and press the √ button; the calculator instantly returns 14. This is the most convenient method for everyday use.
Beyond the Calculation: Applications of Square Roots
The seemingly simple calculation of the square root of 196 opens doors to a wide range of applications across numerous fields:
1. Geometry and Measurement: Calculating Areas and Distances
Square roots are fundamental to geometric calculations. For example:
- Area of a square: If the area of a square is 196 square units, then the length of each side is √196 = 14 units.
- Pythagorean Theorem: This theorem, a cornerstone of geometry, states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides (a² + b² = c²). Finding the length of a side often requires calculating a square root.
- Distance calculations: In coordinate geometry, determining distances between points often involves calculating square roots.
2. Physics and Engineering: Understanding Motion and Forces
Square roots appear frequently in physics formulas:
- Velocity calculations: Many equations related to velocity and acceleration involve square roots. For example, the equation for escape velocity includes a square root term.
- Energy calculations: Kinetic energy (energy of motion) is proportional to the square of the velocity. Finding the velocity from the kinetic energy involves taking a square root.
- Electrical Engineering: Calculations related to impedance in AC circuits involve square roots.
3. Statistics and Probability: Analyzing Data and Risk
Square roots play a vital role in statistical analysis:
- Standard deviation: This measure of data dispersion involves taking the square root of the variance. Standard deviation is critical for understanding the spread of a dataset.
- Root Mean Square (RMS): This value is used to represent the effective value of a varying quantity (e.g., alternating current), requiring the calculation of a square root.
4. Computer Graphics and Game Development: Creating Realistic Visuals
Square roots are essential for vector calculations in computer graphics:
- Distance calculations between points: Rendering 3D graphics relies heavily on distance calculations between points in space, which frequently involve square roots.
- Normalization of vectors: Normalizing vectors (making them unit length) requires dividing by the magnitude, often involving square roots.
5. Finance and Investment: Calculating Returns and Risk
Square roots are employed in financial modeling:
- Standard deviation of returns: In portfolio management, the standard deviation of returns measures the volatility of an investment.
- Option pricing models: Some option pricing models (e.g., Black-Scholes) utilize square roots in their formulas.
Conclusion: The Square Root of 196 and Beyond
While the answer to "What is the square root of 196?" is simply 14, the broader understanding of square roots reveals their significance in a multitude of disciplines. From basic geometry to advanced physics and finance, the ability to calculate and comprehend square roots is a fundamental skill with far-reaching applications. This article aimed to not only provide the answer but also to illuminate the mathematical concepts and practical uses behind this seemingly simple calculation, encouraging a deeper appreciation for the power and relevance of square roots in our world.
Latest Posts
Latest Posts
-
An Atom Gets An Overall Positive Charge By
Mar 28, 2025
-
Hydrogen Metal Or Nonmetal Or Metalloid
Mar 28, 2025
-
List The First 5 Multiples Of 2
Mar 28, 2025
-
How Many Liters In 2 Gallons
Mar 28, 2025
-
How Do You Find The Reciprocal Of A Mixed Fraction
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root 196 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
