How Do You Find The Reciprocal Of A Mixed Fraction
Juapaving
Mar 28, 2025 · 5 min read
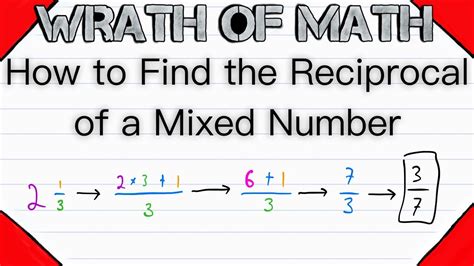
Table of Contents
How to Find the Reciprocal of a Mixed Fraction
Finding the reciprocal of a mixed fraction might seem daunting at first, but it's a straightforward process once you understand the underlying principles. This comprehensive guide will walk you through the steps, explaining the concepts clearly and providing ample examples to solidify your understanding. We'll cover everything from the definition of reciprocals and mixed fractions to advanced applications and common pitfalls to avoid. By the end, you'll be confident in your ability to find the reciprocal of any mixed fraction.
Understanding Reciprocals and Mixed Fractions
Before diving into the process, let's clarify the key terms:
Reciprocal: The reciprocal of a number is simply 1 divided by that number. It's also known as the multiplicative inverse because when you multiply a number by its reciprocal, the result is always 1. For example, the reciprocal of 5 is 1/5 (because 5 * 1/5 = 1), and the reciprocal of 2/3 is 3/2 (because 2/3 * 3/2 = 1).
Mixed Fraction: A mixed fraction combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). For example, 2 1/3, 5 2/7, and 1 3/4 are all mixed fractions.
Step-by-Step Guide: Finding the Reciprocal of a Mixed Fraction
The process of finding the reciprocal of a mixed fraction involves three main steps:
Step 1: Convert the Mixed Fraction to an Improper Fraction
This is the crucial first step. An improper fraction has a numerator that is greater than or equal to its denominator. To convert a mixed fraction to an improper fraction, follow these steps:
- Multiply the whole number by the denominator of the fraction: This gives you the total number of parts represented by the whole number.
- Add the numerator of the fraction to the result from step 1: This gives you the total number of parts in the improper fraction's numerator.
- Keep the same denominator as the original fraction: The denominator remains unchanged.
Example: Let's convert the mixed fraction 2 1/3 to an improper fraction:
- Multiply the whole number (2) by the denominator (3): 2 * 3 = 6
- Add the numerator (1) to the result: 6 + 1 = 7
- Keep the same denominator (3): The improper fraction is 7/3
Step 2: Find the Reciprocal of the Improper Fraction
Once you have an improper fraction, finding its reciprocal is easy: simply swap the numerator and the denominator.
Example: The reciprocal of 7/3 is 3/7.
Step 3: Simplify (If Necessary)
Sometimes, the reciprocal you obtain might be an improper fraction that can be simplified. To simplify, find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD.
Example: Let's say we had a mixed fraction that resulted in a reciprocal of 12/6. The GCD of 12 and 6 is 6. Dividing both the numerator and denominator by 6 gives us 2/1, which simplifies to 2.
Worked Examples
Let's work through a few examples to solidify your understanding:
Example 1: Find the reciprocal of 3 2/5.
- Convert to an improper fraction: (3 * 5) + 2 = 17. The improper fraction is 17/5.
- Find the reciprocal: The reciprocal of 17/5 is 5/17.
- Simplify: 5/17 is already in its simplest form.
Therefore, the reciprocal of 3 2/5 is 5/17.
Example 2: Find the reciprocal of 1 1/4.
- Convert to an improper fraction: (1 * 4) + 1 = 5. The improper fraction is 5/4.
- Find the reciprocal: The reciprocal of 5/4 is 4/5.
- Simplify: 4/5 is already in its simplest form.
Therefore, the reciprocal of 1 1/4 is 4/5.
Example 3: Find the reciprocal of 4 1/2.
- Convert to an improper fraction: (4 * 2) + 1 = 9. The improper fraction is 9/2.
- Find the reciprocal: The reciprocal of 9/2 is 2/9.
- Simplify: 2/9 is already in its simplest form.
Therefore, the reciprocal of 4 1/2 is 2/9.
Example 4 (with simplification): Find the reciprocal of 2 4/6
- Convert to an improper fraction: (2 * 6) + 4 = 16. The improper fraction is 16/6.
- Find the reciprocal: The reciprocal of 16/6 is 6/16.
- Simplify: The GCD of 6 and 16 is 2. Dividing both by 2 gives 3/8.
Therefore, the reciprocal of 2 4/6 is 3/8.
Common Mistakes to Avoid
- Forgetting to convert to an improper fraction: This is the most common mistake. You must convert the mixed fraction to an improper fraction before finding the reciprocal.
- Incorrectly converting to an improper fraction: Double-check your multiplication and addition when converting.
- Not simplifying the reciprocal: Always simplify your answer to its simplest form.
Applications of Reciprocals
Understanding reciprocals is crucial in various mathematical applications, including:
- Division of fractions: Dividing by a fraction is the same as multiplying by its reciprocal.
- Solving equations: Reciprocals are used to isolate variables in algebraic equations.
- Working with ratios and proportions: Reciprocals help in finding equivalent ratios.
- Geometry and trigonometry: Reciprocals are used in various trigonometric functions and geometric calculations.
Conclusion
Finding the reciprocal of a mixed fraction is a fundamental skill in mathematics. By following the three steps outlined in this guide – converting to an improper fraction, finding the reciprocal, and simplifying – you can confidently tackle any mixed fraction. Remember to practice regularly to reinforce your understanding and avoid common mistakes. With consistent practice, this process will become second nature. Mastering this skill opens doors to more advanced mathematical concepts and applications.
Latest Posts
Latest Posts
-
Would Silver React With Dilute Sulfuric Acid
Mar 31, 2025
-
How Many Factors Does A Composite Number Have
Mar 31, 2025
-
What Is 4 The Square Root Of
Mar 31, 2025
-
Tendons And Ligaments Are Examples Of
Mar 31, 2025
-
What Is A Perfect Cube In Mathematics
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Do You Find The Reciprocal Of A Mixed Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
