What Is The Prime Factorization Of 96
Juapaving
Apr 04, 2025 · 5 min read
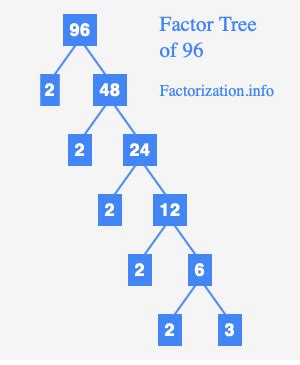
Table of Contents
What is the Prime Factorization of 96? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What is the prime factorization of 96?" opens a door to a fascinating world of number theory, prime numbers, and the fundamental building blocks of mathematics. While the answer itself is relatively straightforward, understanding the process and the underlying concepts provides valuable insight into how numbers are structured and how prime factorization plays a crucial role in various mathematical fields. This article will not only answer the question directly but also explore the broader concepts of prime numbers, factorization, and their applications.
Understanding Prime Numbers
Before diving into the prime factorization of 96, let's establish a firm understanding of what prime numbers are. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's a number that can only be divided evenly by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. Prime numbers are considered the fundamental building blocks of all other natural numbers because every natural number greater than 1 can be expressed as a unique product of prime numbers. This is the cornerstone of the Fundamental Theorem of Arithmetic.
Identifying Prime Numbers
Identifying prime numbers can be a challenge, especially as the numbers get larger. While there's no single, easy formula to determine if a number is prime, several methods can help:
-
Trial Division: This method involves testing divisibility by all prime numbers less than the square root of the number in question. If the number isn't divisible by any of these primes, it's prime. This method becomes less efficient as the numbers increase in size.
-
Sieve of Eratosthenes: This ancient algorithm is a more efficient way to find all prime numbers up to a specified limit. It works by iteratively marking multiples of prime numbers as composite (non-prime).
-
Primality Tests: For very large numbers, sophisticated primality tests are used. These tests use advanced mathematical principles to determine primality with a high degree of certainty.
Prime Factorization: Breaking Down Numbers
Prime factorization is the process of expressing a composite number (a number that is not prime) as a product of its prime factors. This process is unique for every composite number, meaning there's only one way to represent a number as a product of prime factors (ignoring the order of the factors). This uniqueness is a crucial aspect of the Fundamental Theorem of Arithmetic.
The Process of Prime Factorization
The process of prime factorization typically involves repeatedly dividing the number by the smallest prime number that divides it evenly. This process is continued until the result is 1. The prime numbers used in the divisions are the prime factors of the original number.
Finding the Prime Factorization of 96
Now, let's apply the process to find the prime factorization of 96:
-
Start with the smallest prime number, 2: 96 is an even number, so it's divisible by 2. 96 ÷ 2 = 48.
-
Continue with 2: 48 is also divisible by 2. 48 ÷ 2 = 24.
-
Continue with 2: 24 is divisible by 2. 24 ÷ 2 = 12.
-
Continue with 2: 12 is divisible by 2. 12 ÷ 2 = 6.
-
Continue with 2: 6 is divisible by 2. 6 ÷ 2 = 3.
-
Finally, we reach a prime number: 3 is a prime number. Therefore, the prime factorization of 96 is 2 x 2 x 2 x 2 x 2 x 3.
Representing the Prime Factorization
The prime factorization of 96 can be written more concisely using exponents: 2<sup>5</sup> x 3. This means that 96 is the product of five 2s and one 3.
Applications of Prime Factorization
Prime factorization might seem like a purely theoretical concept, but it has numerous practical applications in various fields:
-
Cryptography: Modern cryptography relies heavily on prime numbers and their properties. RSA encryption, one of the most widely used encryption algorithms, uses very large prime numbers to secure online transactions and communications. The difficulty of factoring large numbers into their prime components forms the basis of the security of these systems.
-
Computer Science: Prime factorization is used in various algorithms and data structures in computer science. For example, it's used in hash table implementations and certain types of sorting algorithms.
-
Number Theory: Prime factorization is fundamental to many areas of number theory, including the study of modular arithmetic, Diophantine equations, and the distribution of prime numbers.
-
Coding Theory: Prime numbers are crucial in error-correcting codes, which are used to detect and correct errors in data transmission and storage.
Beyond the Basics: Exploring Further Concepts
The prime factorization of 96 provides a springboard for exploring more advanced concepts in number theory:
-
Greatest Common Divisor (GCD): The GCD of two or more numbers is the largest number that divides all of them evenly. Prime factorization is a useful tool for finding the GCD, as it allows you to identify the common prime factors and their lowest powers.
-
Least Common Multiple (LCM): The LCM of two or more numbers is the smallest number that is a multiple of all of them. Similar to the GCD, prime factorization simplifies the process of finding the LCM.
-
Modular Arithmetic: Modular arithmetic, where numbers "wrap around" after reaching a certain modulus, is widely used in cryptography and computer science. Prime numbers play a significant role in understanding modular arithmetic.
Conclusion: The Importance of Prime Factorization
While finding the prime factorization of 96 might seem like a simple task, it highlights the fundamental importance of prime numbers in mathematics and its applications. The process of prime factorization, rooted in the Fundamental Theorem of Arithmetic, underpins many crucial aspects of modern technology and advanced mathematical concepts. Understanding this process provides valuable insight into the structure of numbers and their inherent properties, showcasing the beauty and power of fundamental mathematical principles. The seemingly simple question of 96's prime factorization opens a window into a vast and fascinating world of mathematical exploration.
Latest Posts
Latest Posts
-
50 Is What Percent Of 500
Apr 05, 2025
-
Maths Multiplication Tables From 11 To 20
Apr 05, 2025
-
What Is The Electron Configuration Of Bromine
Apr 05, 2025
-
How Many Players Are On A Cricket Team
Apr 05, 2025
-
Difference Between Baking Soda And Baking Powder Chemical Formula
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization Of 96 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
