50 Is What Percent Of 500
Juapaving
Apr 05, 2025 · 5 min read
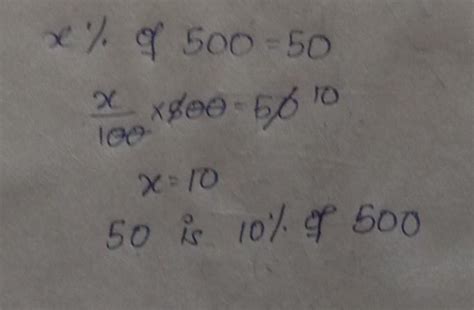
Table of Contents
50 is What Percent of 500? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This comprehensive guide delves into the question, "50 is what percent of 500?", providing not just the answer but a thorough understanding of the underlying principles and methods for solving percentage problems. We'll explore different approaches, tackle related scenarios, and offer practical applications to solidify your grasp of this crucial mathematical concept.
Understanding Percentages: The Basics
Before diving into the specific problem, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "out of 100" or "per hundred." For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Calculating "50 is What Percent of 500?"
There are several methods to determine what percentage 50 represents of 500. Let's explore three common approaches:
Method 1: The Proportion Method
This method involves setting up a proportion, equating two ratios. We know that the part (50) is related to the whole (500), and we want to find the percentage (x). The proportion can be expressed as:
50/500 = x/100
To solve for 'x', we cross-multiply:
50 * 100 = 500 * x
5000 = 500x
Now, divide both sides by 500:
x = 5000/500
x = 10
Therefore, 50 is 10% of 500.
Method 2: The Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
First, express the relationship as a fraction:
50/500
Simplify the fraction:
1/10
Convert the fraction to a decimal by dividing the numerator by the denominator:
1 ÷ 10 = 0.1
Finally, multiply the decimal by 100 to obtain the percentage:
0.1 * 100 = 10%
So, once again, we confirm that 50 is 10% of 500.
Method 3: The Formula Method
A more direct approach is to use the percentage formula:
Percentage = (Part / Whole) * 100
In this case:
Part = 50
Whole = 500
Substitute these values into the formula:
Percentage = (50 / 500) * 100
Percentage = 0.1 * 100
Percentage = 10%
This confirms, for the third time, that 50 represents 10% of 500.
Practical Applications and Real-World Examples
The ability to calculate percentages has wide-ranging practical applications. Here are some examples:
1. Sales and Discounts
Imagine a store offers a 10% discount on a $500 item. Using the knowledge gained above, you can quickly calculate the discount amount:
Discount = 10% of $500 = (0.1 * 500) = $50
The final price after the discount would be:
Final Price = $500 - $50 = $450
2. Tax Calculations
Understanding percentages is crucial for calculating taxes. If the sales tax rate is 6%, and you purchase an item for $500, the tax amount would be:
Tax Amount = 6% of $500 = (0.06 * 500) = $30
The total cost, including tax, would be:
Total Cost = $500 + $30 = $530
3. Grade Calculations
Percentages are frequently used to represent grades in academic settings. If a student scores 50 points out of a possible 500 points on an exam, their percentage score is:
Percentage Score = (50 / 500) * 100 = 10%
4. Financial Analysis
In finance, percentages are essential for analyzing financial statements. For instance, if a company's net profit is $50 million out of a total revenue of $500 million, the net profit margin is:
Net Profit Margin = (50 / 500) * 100 = 10%
5. Data Analysis and Statistics
Percentages play a vital role in representing and interpreting data. For example, if a survey of 500 people reveals that 50 prefer a particular product, this represents:
Percentage Preference = (50 / 500) * 100 = 10%
This percentage helps researchers understand the level of preference for that particular product within the surveyed population.
Beyond the Basics: More Complex Percentage Problems
While the problem "50 is what percent of 500?" is relatively straightforward, understanding the underlying principles allows you to tackle more complex percentage calculations. These might involve:
- Finding the whole: If you know a percentage and the part, you can calculate the whole. For example, if 10% of a number is 50, what is the number? This can be solved by reversing the percentage formula.
- Finding the part: If you know a percentage and the whole, you can find the part. For example, what is 25% of 500? This involves a straightforward multiplication.
- Percentage increase/decrease: Calculating percentage changes involves finding the difference between two numbers and then expressing it as a percentage of the original number. This is common in scenarios involving sales, inflation, or population growth.
- Compound percentages: These involve applying percentages multiple times, such as compound interest calculations. These require a more advanced understanding of exponential growth.
Mastering the fundamental principles of percentage calculations, like those used to solve "50 is what percent of 500?", is crucial for tackling these more complex problems. The core concepts remain the same – understanding the relationship between the part, the whole, and the percentage.
Conclusion: Mastering Percentages for Everyday Life
The ability to calculate percentages is a valuable skill applicable across many aspects of daily life. Whether it's calculating discounts, taxes, grades, or analyzing financial data, a solid understanding of percentages is essential for informed decision-making. By understanding the different methods and practicing their application, you can confidently tackle various percentage-related problems and improve your overall quantitative literacy. The simple question, "50 is what percent of 500?" serves as a powerful gateway to mastering this crucial mathematical concept. Remember the key methods outlined here – the proportion method, the decimal method, and the formula method – and you'll be well-equipped to handle a wide array of percentage calculations in your personal and professional life.
Latest Posts
Latest Posts
-
What Does Vitamin A B C And D Do
Apr 05, 2025
-
How To Write 1850 00 On A Check
Apr 05, 2025
-
How To Calculate A Perimeter Of A Triangle
Apr 05, 2025
-
What Is Xx11 In Roman Numerals
Apr 05, 2025
-
What Is A Shape Called With 11 Sides
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about 50 Is What Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
