What Is The Prime Factorization For 44
Juapaving
Mar 21, 2025 · 6 min read
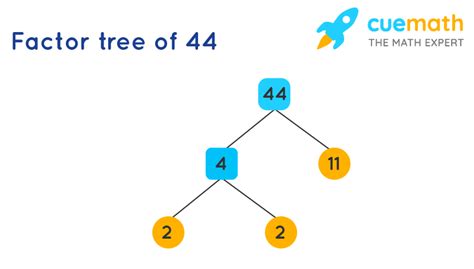
Table of Contents
- What Is The Prime Factorization For 44
- Table of Contents
- Decomposing 44: A Deep Dive into Prime Factorization
- What is Prime Factorization?
- Finding the Prime Factors of 44
- Visualizing with a Factor Tree
- Beyond the Factor Tree: Other Methods
- The Significance of Prime Factorization
- Exploring the Properties of the Prime Factors of 44
- Prime Factorization and the Fundamental Theorem of Arithmetic
- Applications in Real-World Scenarios
- Further Exploration: Beyond 44
- Conclusion: The Enduring Importance of Prime Factorization
- Latest Posts
- Latest Posts
- Related Post
Decomposing 44: A Deep Dive into Prime Factorization
Prime factorization. It sounds intimidating, like some arcane mathematical ritual. But the truth is, understanding prime factorization is fundamental to grasping many core concepts in number theory and algebra. And while the process itself is simple, the underlying principles are surprisingly rich. Today, we'll explore the prime factorization of 44, using it as a springboard to understand the broader world of prime numbers and their unique properties.
What is Prime Factorization?
Before we tackle 44, let's clarify what prime factorization is. Simply put, it's the process of breaking down a composite number (a number greater than 1 that's not prime) into its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. They're the building blocks of all other whole numbers.
Prime factorization is unique; every composite number has only one set of prime factors, regardless of the order in which you find them. This uniqueness is a cornerstone of many mathematical proofs and algorithms.
Finding the Prime Factors of 44
Now, let's find the prime factorization of 44. We can do this using a method called the factor tree.
-
Start with the number: We begin with 44.
-
Find the smallest prime factor: The smallest prime number is 2. 44 is clearly divisible by 2 (since it's an even number). So, we divide 44 by 2, getting 22.
-
Continue factoring: Now we have 2 and 22. 2 is already a prime number, but 22 is not. Again, 22 is divisible by 2, giving us 11.
-
Identify the prime factors: We've now reached 2, 2, and 11. All three numbers are prime. We've successfully broken 44 down into its prime factors.
Therefore, the prime factorization of 44 is 2 x 2 x 11, or 2² x 11.
Visualizing with a Factor Tree
A factor tree provides a visual representation of this process:
44
/ \
2 22
/ \
2 11
This tree shows the step-by-step breakdown of 44 into its prime factors. Each branch represents a division by a prime number, until we're left with only prime numbers at the bottom.
Beyond the Factor Tree: Other Methods
While the factor tree is a visually intuitive method, especially for smaller numbers, other techniques exist for finding prime factorizations. For larger numbers, these alternative approaches can be more efficient:
-
Division by Primes: This method involves systematically dividing the number by each prime number, starting with 2, then 3, 5, 7, and so on, until you reach 1. Each time a prime number divides the number evenly, you've found a prime factor.
-
Using Algorithms: For very large numbers, sophisticated algorithms are employed. These algorithms leverage advanced mathematical principles to efficiently determine prime factorization, which is crucial in cryptography. The complexity of these algorithms is a testament to the intricate nature of prime numbers.
The Significance of Prime Factorization
The seemingly simple act of finding prime factors has far-reaching implications in various fields:
-
Cryptography: The security of many encryption systems relies on the difficulty of factoring very large numbers into their prime components. The larger the number, the exponentially harder it becomes to find its prime factors, making these systems highly secure.
-
Number Theory: Prime factorization is a fundamental concept in number theory, forming the basis for many theorems and proofs. Understanding the distribution and properties of prime numbers is a continuous area of research in mathematics.
-
Algebra: Prime factorization plays a crucial role in simplifying algebraic expressions and solving equations. Factoring polynomials, for instance, often involves finding the prime factors of the coefficients.
-
Computer Science: Algorithms related to prime factorization are used in various computer science applications, including data compression and efficient data storage.
Exploring the Properties of the Prime Factors of 44
Let's delve a bit deeper into the specific prime factors of 44 – 2 and 11.
-
2: The only even prime number: 2 is unique amongst prime numbers because it's the only even prime. All other even numbers are composite, as they're divisible by 2. This makes 2 a particularly important prime in number theory.
-
11: A prime number in its own right: 11 is a prime number, meaning it's only divisible by 1 and itself. It's part of the infinite sequence of prime numbers, a fact that has fascinated mathematicians for centuries.
The combination of 2 and 11, in the factorization of 44, highlights the fundamental building blocks of composite numbers.
Prime Factorization and the Fundamental Theorem of Arithmetic
The fact that 44 has only one unique prime factorization (2² x 11) isn't just a coincidence. It's a consequence of the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers, disregarding the order of the factors. This theorem is a bedrock of number theory, providing a foundational understanding of the structure of integers.
Applications in Real-World Scenarios
While prime factorization might seem abstract, it has tangible applications in various everyday scenarios, albeit often indirectly:
-
Data Compression: Efficient data compression algorithms often utilize prime factorization principles to reduce redundancy and optimize storage space.
-
Error Correction Codes: Prime numbers play a role in creating robust error correction codes, which ensure data integrity during transmission or storage.
-
Hashing Algorithms: Hashing functions, used extensively in computer science for data integrity and security checks, sometimes rely on prime numbers for their effectiveness.
Further Exploration: Beyond 44
Understanding the prime factorization of 44 opens the door to exploring the vast world of prime numbers and their properties. You can extend your understanding by:
-
Factoring larger numbers: Try factoring larger composite numbers using the methods discussed above. This will improve your understanding of the process and its challenges.
-
Investigating prime number patterns: Research the distribution of prime numbers and explore conjectures about their patterns. The Riemann Hypothesis, for example, is one of the most important unsolved problems in mathematics, related to the distribution of prime numbers.
-
Learning more about number theory: Delve into the rich world of number theory, exploring topics such as modular arithmetic, Diophantine equations, and other fascinating areas.
Conclusion: The Enduring Importance of Prime Factorization
The seemingly simple task of finding the prime factorization of 44 has led us on a journey through the fundamental concepts of number theory and its applications in various fields. From cryptography to computer science, prime factorization plays a crucial role in shaping our technological world. While we started with a seemingly simple number, the principles we've explored have profound implications and continue to fascinate mathematicians and computer scientists alike. So, the next time you encounter a composite number, remember the power and elegance of prime factorization.
Latest Posts
Latest Posts
-
What Can 51 Be Divided By
Mar 28, 2025
-
What Occupies Space And Has Mass
Mar 28, 2025
-
Equation Of A Line Parallel To The Y Axis
Mar 28, 2025
-
Choose The Best Reagents To Complete The Reaction Shown Below
Mar 28, 2025
-
Do Generators Produce Ac Or Dc
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization For 44 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
