What Can 51 Be Divided By
Juapaving
Mar 28, 2025 · 5 min read
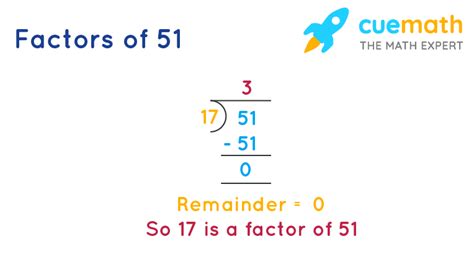
Table of Contents
What Can 51 Be Divided By? A Deep Dive into Divisibility and Prime Factorization
The seemingly simple question, "What can 51 be divided by?" opens a door to a fascinating world of number theory, divisibility rules, prime factorization, and even a touch of abstract algebra. While the immediate answer might seem straightforward, exploring the underlying concepts reveals a wealth of mathematical richness. This article will delve into the different ways to determine the divisors of 51, explaining the methods in a clear and accessible way, suitable for both beginners and those seeking a deeper understanding.
Understanding Divisibility
Before tackling 51 specifically, let's establish a foundational understanding of divisibility. A number a is divisible by a number b if the result of a divided by b is a whole number (an integer) with no remainder. In other words, a/b = k, where k is an integer. This means b is a factor or divisor of a.
For example:
- 12 is divisible by 3 (12/3 = 4)
- 20 is divisible by 5 (20/5 = 4)
- 15 is divisible by 15 (15/15 = 1)
This seemingly simple concept forms the bedrock of many advanced mathematical ideas.
Finding the Divisors of 51: A Systematic Approach
Now, let's focus on 51. We can approach finding its divisors in several ways:
1. Brute Force Method (Trial Division)
This is the most straightforward method. We systematically check every integer from 1 up to 51 to see if it divides 51 without leaving a remainder. This works, but it can be tedious for larger numbers.
Let's try it for 51:
- 1 divides 51 (51/1 = 51)
- 2 does not divide 51 (51/2 = 25.5)
- 3 divides 51 (51/3 = 17)
- 17 divides 51 (51/17 = 3)
- Other numbers between 1 and 51 won't divide 51 evenly.
Therefore, the divisors of 51 are 1, 3, 17, and 51.
2. Utilizing Divisibility Rules
Divisibility rules offer shortcuts for determining divisibility by certain numbers. For example:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, 8). 51 is not divisible by 2.
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. For 51, 5 + 1 = 6, which is divisible by 3. Thus, 51 is divisible by 3.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5. 51 is not divisible by 5.
- Divisibility by 17: There isn't a simple rule for 17, but we know from trial division that 51 is divisible by 17.
3. Prime Factorization: The Key to Understanding Divisibility
Prime factorization is the most powerful technique for finding all the divisors of a number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11, 13, 17...). Prime factorization involves expressing a number as a product of its prime factors.
To find the prime factorization of 51:
- We know 51 is divisible by 3 (from the divisibility rule). 51/3 = 17.
- 17 is a prime number.
Therefore, the prime factorization of 51 is 3 x 17.
Once you have the prime factorization, finding all the divisors becomes straightforward. You systematically create all possible combinations of the prime factors and their powers.
For 51 (3 x 17):
- 3⁰ x 17⁰ = 1
- 3¹ x 17⁰ = 3
- 3⁰ x 17¹ = 17
- 3¹ x 17¹ = 51
These are the four divisors of 51.
Beyond Divisors: Exploring Related Concepts
The concept of divisibility lays the groundwork for many other important mathematical ideas:
1. Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
The greatest common divisor (GCD) of two or more numbers is the largest number that divides all of them without leaving a remainder. The least common multiple (LCM) is the smallest number that is a multiple of all the numbers. Finding the GCD and LCM is crucial in various mathematical applications, including simplifying fractions and solving problems in algebra.
For example, let's find the GCD and LCM of 51 and 68.
-
Prime factorization of 51: 3 x 17
-
Prime factorization of 68: 2 x 2 x 17 = 2² x 17
-
GCD: The common prime factor is 17. Therefore, the GCD(51, 68) = 17.
-
LCM: The LCM includes all prime factors raised to their highest powers present in either factorization: 2² x 3 x 17 = 204. Therefore, LCM(51,68) = 204
2. Modular Arithmetic and Congruence
Modular arithmetic deals with remainders after division. We say that a is congruent to b modulo m (written as a ≡ b (mod m) ) if a and b have the same remainder when divided by m. This is fundamental in cryptography and computer science.
For instance, 51 ≡ 0 (mod 3) because 51 has a remainder of 0 when divided by 3. 51 ≡ 2 (mod 5) because 51 has a remainder of 2 when divided by 5.
3. Abstract Algebra and Group Theory
Divisibility and prime factorization play a vital role in abstract algebra, particularly in group theory. Groups are algebraic structures with specific properties, and understanding the divisors of numbers is essential for analyzing certain group structures. This is a more advanced topic but demonstrates the far-reaching implications of seemingly simple concepts like divisibility.
Conclusion: The Significance of Divisibility
The seemingly simple question of what 51 can be divided by leads to a deeper understanding of core mathematical concepts. From the basic trial division method to the elegant power of prime factorization, understanding divisibility is essential for various mathematical explorations. This extends beyond simple division problems into more advanced areas like modular arithmetic and abstract algebra, showcasing the interconnectedness and profound depth of mathematical theory. The divisors of 51, seemingly insignificant on their own, represent a gateway to a richer appreciation of the mathematical world.
Latest Posts
Latest Posts
-
5 Levels Of Organization In An Ecosystem
Mar 31, 2025
-
Would Silver React With Dilute Sulfuric Acid
Mar 31, 2025
-
How Many Factors Does A Composite Number Have
Mar 31, 2025
-
What Is 4 The Square Root Of
Mar 31, 2025
-
Tendons And Ligaments Are Examples Of
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Can 51 Be Divided By . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
