Equation Of A Line Parallel To The Y Axis
Juapaving
Mar 28, 2025 · 6 min read
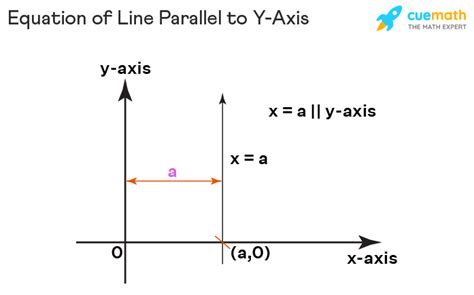
Table of Contents
The Equation of a Line Parallel to the Y-Axis: A Comprehensive Guide
The equation of a line parallel to the y-axis is a fundamental concept in coordinate geometry. Understanding this equation is crucial for solving various mathematical problems and visualizing geometrical relationships on a Cartesian plane. This comprehensive guide delves into the equation, its derivation, applications, and related concepts, providing a thorough understanding for students and enthusiasts alike.
Understanding the Cartesian Plane and Linear Equations
Before diving into the specifics of lines parallel to the y-axis, let's establish a solid foundation. The Cartesian plane, also known as the coordinate plane, is a two-dimensional surface formed by two perpendicular number lines, the x-axis and the y-axis. These axes intersect at a point called the origin (0,0). Any point on this plane can be uniquely identified by its coordinates (x, y), where 'x' represents the horizontal distance from the y-axis and 'y' represents the vertical distance from the x-axis.
Linear equations represent straight lines on the Cartesian plane. The general form of a linear equation is Ax + By = C, where A, B, and C are constants. However, different forms of linear equations exist, each providing unique insights into the line's characteristics. The most common forms are:
- Slope-intercept form: y = mx + b, where 'm' is the slope and 'b' is the y-intercept (the point where the line intersects the y-axis).
- Point-slope form: y - y₁ = m(x - x₁), where 'm' is the slope and (x₁, y₁) is a point on the line.
- Standard form: Ax + By = C, where A, B, and C are integers.
The Unique Case of Vertical Lines: Parallel to the Y-Axis
Lines parallel to the y-axis are unique because they have an undefined slope. Let's explore why:
The slope of a line is defined as the change in y divided by the change in x (rise over run), or:
m = (y₂ - y₁) / (x₂ - x₁)
For a line parallel to the y-axis, all points on the line share the same x-coordinate. This means that x₂ - x₁ will always equal zero. Dividing by zero is undefined in mathematics, hence the undefined slope. This is why the slope-intercept and point-slope forms cannot be directly used to represent these lines.
The Equation: x = k
The equation of a line parallel to the y-axis takes the simple form:
x = k
where 'k' is a constant representing the x-coordinate of every point on the line. This means that no matter what the y-coordinate is, the x-coordinate will always be 'k'.
Why this works: Consider the points (2, 1), (2, 3), and (2, -2). All these points lie on the same vertical line, and their x-coordinate is always 2. Therefore, the equation of this line is x = 2. Similarly, any line parallel to the y-axis can be represented by x = k, where k is the x-intercept (the point where the line crosses the x-axis).
Visualizing the Equation
Imagine plotting several points with the same x-coordinate, say x = 3. You might have points like (3, 1), (3, 0), (3, -1), (3, 2), and so on. If you plot these points on the Cartesian plane and connect them, you'll get a perfectly vertical line passing through the point (3, 0) on the x-axis. This line is parallel to the y-axis and its equation is x = 3.
Applications and Examples
The equation x = k has several practical applications:
- Graphing: Quickly plot a vertical line knowing its x-intercept.
- Finding intersections: Determine the point of intersection between a vertical line and other lines or curves.
- Solving systems of equations: Combine the equation x = k with other equations to find the solution to a system.
- Real-world modeling: Representing scenarios where a specific value remains constant regardless of another variable. For instance, the equation might represent a building's fixed longitude in a geographic coordinate system.
Example 1:
Find the equation of the line parallel to the y-axis that passes through the point (5, 2).
Since the line is parallel to the y-axis, its equation is of the form x = k. The x-coordinate of the given point is 5, so the equation of the line is x = 5.
Example 2:
Find the point of intersection between the line x = 4 and the line y = 2x - 1.
Substitute x = 4 into the second equation:
y = 2(4) - 1 = 7
Therefore, the point of intersection is (4, 7).
Example 3:
A vertical fence is built along the line x = -2. What is the equation of the fence?
The equation representing the fence is simply x = -2.
Distinguishing between Vertical and Horizontal Lines
It's crucial to distinguish between lines parallel to the y-axis (vertical lines) and lines parallel to the x-axis (horizontal lines).
- Vertical lines (parallel to the y-axis): Have an undefined slope and their equation is x = k, where k is a constant.
- Horizontal lines (parallel to the x-axis): Have a slope of zero and their equation is y = k, where k is a constant.
The key difference lies in the constant term: 'x' for vertical lines and 'y' for horizontal lines.
Advanced Concepts and Extensions
The understanding of the equation x = k forms the basis for more complex concepts in coordinate geometry:
- Distance between a point and a line: Calculating the shortest distance between a point and a vertical line involves using the formula for the distance between a point and a line, considering that the line has an undefined slope.
- Systems of equations with vertical lines: Solving systems of linear equations that include a vertical line often involves substitution, directly solving for the x-coordinate using the equation x = k, and then substituting this value into the other equation(s) to find the y-coordinate.
- Lines in three-dimensional space: The concept of a vertical line extends to three dimensions, where a line parallel to the z-axis can be represented as x = a and y = b, where 'a' and 'b' are constants.
Conclusion: Mastering the Equation x = k
The equation x = k, representing a line parallel to the y-axis, is a fundamental yet often overlooked concept in coordinate geometry. Understanding its derivation, applications, and the distinction between vertical and horizontal lines is essential for a solid grasp of linear algebra and its applications. By mastering this concept, you build a robust foundation for tackling more advanced mathematical problems and real-world applications requiring spatial reasoning and geometric understanding. Remember the simplicity and power of this seemingly basic equation – it's a cornerstone of understanding lines on the Cartesian plane.
Latest Posts
Latest Posts
-
5 Levels Of Organization In An Ecosystem
Mar 31, 2025
-
Would Silver React With Dilute Sulfuric Acid
Mar 31, 2025
-
How Many Factors Does A Composite Number Have
Mar 31, 2025
-
What Is 4 The Square Root Of
Mar 31, 2025
-
Tendons And Ligaments Are Examples Of
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Equation Of A Line Parallel To The Y Axis . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
