What Is The Lowest Common Multiple Of 3 And 9
Juapaving
Mar 25, 2025 · 5 min read
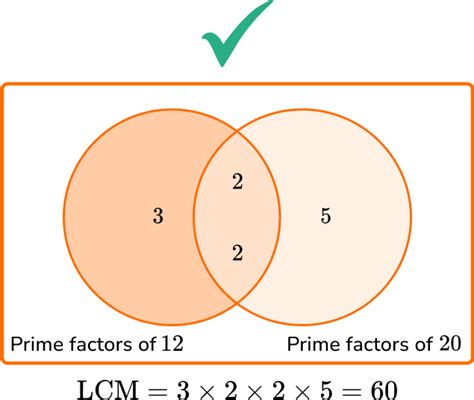
Table of Contents
What is the Lowest Common Multiple (LCM) of 3 and 9? A Deep Dive into Number Theory
Finding the lowest common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles unlocks a deeper appreciation of number theory and its applications in various fields. This article will delve into the concept of LCM, focusing specifically on the LCM of 3 and 9, while exploring different methods for calculating it and demonstrating its relevance in broader mathematical contexts.
Understanding Lowest Common Multiples (LCM)
The lowest common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. It's a fundamental concept in number theory with practical applications in areas ranging from scheduling problems to simplifying fractions. Think of it as finding the smallest number that contains all the numbers you're considering as factors.
For instance, consider the numbers 2 and 3. Their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The common multiples of 2 and 3 are 6, 12, 18, 24, and so on. The lowest common multiple is 6.
Calculating the LCM of 3 and 9: Methods and Approaches
Now, let's focus on finding the LCM of 3 and 9. We can use several methods:
Method 1: Listing Multiples
This is the most straightforward approach, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18...
- Multiples of 9: 9, 18, 27, 36...
The smallest number appearing in both lists is 9. Therefore, the LCM of 3 and 9 is 9.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM using prime factorization, we take the highest power of each prime factor present in the numbers:
The only prime factor is 3, and the highest power is 3². Therefore, the LCM of 3 and 9 is 3² = 9.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula connecting them:
LCM(a, b) * GCD(a, b) = a * b
First, we find the GCD of 3 and 9. The GCD is the largest number that divides both 3 and 9 without leaving a remainder. In this case, the GCD(3, 9) = 3.
Now, we can use the formula:
LCM(3, 9) * GCD(3, 9) = 3 * 9
LCM(3, 9) * 3 = 27
LCM(3, 9) = 27 / 3 = **9**
This method highlights the interconnectedness of LCM and GCD, emphasizing the fundamental relationships within number theory.
The Significance of the LCM: Real-World Applications
While the LCM of 3 and 9 might seem trivial, the concept of LCM has broader applications in various fields:
1. Scheduling Problems
Imagine you have two machines that perform different tasks. Machine A completes its cycle every 3 hours, and Machine B completes its cycle every 9 hours. To find out when both machines will complete their cycles simultaneously, you need to find the LCM(3, 9). The LCM, which is 9 hours, represents the time when both machines will be at the starting point of their cycles simultaneously.
2. Fraction Simplification
When adding or subtracting fractions, finding the LCM of the denominators is crucial for obtaining a common denominator. This simplifies the process of arithmetic operations with fractions.
3. Music Theory
The LCM is used in music theory to determine the least common multiple of different rhythmic patterns, which is essential for understanding complex musical compositions.
4. Modular Arithmetic and Cryptography
LCM plays a vital role in modular arithmetic, a branch of number theory essential for cryptography and computer science. Modular arithmetic deals with remainders after division, and the LCM is often used to find solutions to congruences.
5. Geometric Problems
LCM finds its place in solving problems that involve repeating patterns or cycles in geometry. For instance, tiling problems often require finding the LCM to determine the smallest area that can be perfectly tiled using two or more different tiles.
Expanding on the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. For example, to find the LCM of 3, 6, and 9:
Method 1: Listing Multiples: List the multiples of each number until you find the smallest common multiple.
Method 2: Prime Factorization: Find the prime factorization of each number. Then, take the highest power of each prime factor present in the numbers.
Method 3: Iterative GCD Approach: You can extend the GCD approach iteratively. For example, you would first find the LCM of two numbers, and then find the LCM of that result and the third number, and so on.
Let’s find the LCM of 3, 6, and 9 using prime factorization:
- 3 = 3¹
- 6 = 2¹ * 3¹
- 9 = 3²
The highest power of 2 is 2¹, and the highest power of 3 is 3². Therefore, LCM(3, 6, 9) = 2¹ * 3² = 18.
Conclusion: The Humble LCM and its Powerful Applications
The LCM, even in its simplest form like the LCM of 3 and 9, is a cornerstone concept in number theory with far-reaching consequences. While seemingly basic, understanding its calculation methods and applications deepens one's mathematical understanding and opens doors to solving problems across diverse fields. The exploration of the LCM of 3 and 9 has served as a springboard to understanding more complex number theory concepts and their impact on various aspects of mathematics, computer science, and even music. Mastering the concept of the LCM empowers you to tackle more intricate mathematical challenges and appreciate the beauty of mathematical relationships. From scheduling problems to cryptography, the LCM quietly but powerfully underpins many aspects of our world.
Latest Posts
Latest Posts
-
Salt A Commonly Used In Bakery Products
Mar 28, 2025
-
The Shapes Of The Horizontal Cross Sections
Mar 28, 2025
-
The Largest Gland Of The Body
Mar 28, 2025
-
What Is The Lcm Of 6 8 And 9
Mar 28, 2025
-
If The Diagonals Of A Quadrilateral Bisect Each Other
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lowest Common Multiple Of 3 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
