What Is The Lcm Of 8 And 11
Juapaving
Mar 21, 2025 · 5 min read
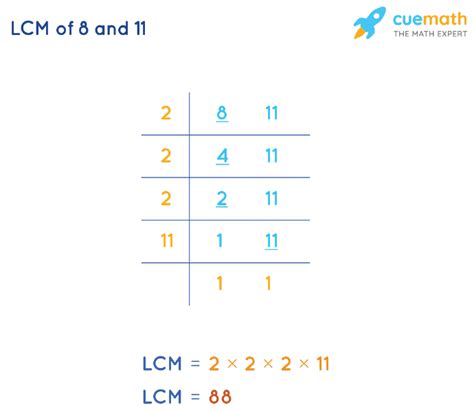
Table of Contents
What is the LCM of 8 and 11? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving problems in various fields like music theory and scheduling. This article will delve into the process of finding the LCM of 8 and 11, exploring different methods and illustrating the underlying principles. We'll also discuss the broader context of LCMs and their importance.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 8 and 11, let's establish a solid understanding of what an LCM is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple, therefore, is 6.
Method 1: Listing Multiples
One straightforward method for finding the LCM is to list the multiples of each number until you find the smallest common multiple. Let's apply this to 8 and 11:
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, ...
Multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, ...
By inspecting the lists, we can see that the smallest number appearing in both lists is 88. Therefore, the LCM of 8 and 11 is 88.
This method works well for smaller numbers, but it can become cumbersome and time-consuming for larger numbers. Let's explore more efficient methods.
Method 2: Prime Factorization
A more efficient and widely applicable method involves finding the prime factorization of each number. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 11: 11 (11 is a prime number)
To find the LCM using prime factorization, we follow these steps:
- Identify the prime factors: We have 2 and 11.
- Find the highest power of each prime factor: The highest power of 2 is 2³ (from the factorization of 8), and the highest power of 11 is 11¹ (from the factorization of 11).
- Multiply the highest powers together: LCM(8, 11) = 2³ x 11 = 8 x 11 = 88
This method is significantly more efficient, especially when dealing with larger numbers or multiple numbers. It provides a systematic approach that avoids the need for extensive listing of multiples.
Method 3: Using the Formula (for two numbers)
For two numbers, a and b, there's a handy formula that relates the LCM and the greatest common divisor (GCD):
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- LCM(a, b) is the least common multiple of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
- |a x b| represents the absolute value of the product of a and b.
Let's apply this to 8 and 11:
-
Find the GCD of 8 and 11: The greatest common divisor of 8 and 11 is 1, as they share no common factors other than 1.
-
Apply the formula: LCM(8, 11) = (8 x 11) / GCD(8, 11) = 88 / 1 = 88
This method requires finding the GCD first, which can be done using various techniques, including the Euclidean algorithm. However, for relatively small numbers like 8 and 11, it's relatively straightforward.
The Significance of LCMs
The concept of least common multiples has numerous applications across various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators.
-
Scheduling and Timing: LCMs are crucial in scheduling problems. For instance, if two events occur at intervals of 8 days and 11 days respectively, the LCM (88 days) represents the number of days after which both events will occur on the same day again.
-
Music Theory: The LCM plays a role in determining the least common denominator for musical rhythms and time signatures.
-
Modular Arithmetic: The LCM is used in solving congruences and related problems in number theory.
-
Computer Science: LCMs appear in various algorithms and programming problems related to cyclic processes or scheduling.
Relating LCM and GCD: A Deeper Dive
The relationship between the LCM and GCD of two numbers, a and b, is fundamental:
LCM(a, b) * GCD(a, b) = |a * b|
This equation highlights the inherent connection between these two concepts. Understanding this relationship provides a powerful tool for solving problems involving both LCM and GCD.
Finding the LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly well-suited for this:
- Find the prime factorization of each number.
- Identify the highest power of each prime factor present in any of the factorizations.
- Multiply the highest powers together to find the LCM.
Conclusion: The LCM of 8 and 11 is 88
Through various methods, we've definitively established that the least common multiple of 8 and 11 is 88. Understanding the different approaches—listing multiples, prime factorization, and using the LCM/GCD formula—provides a versatile toolkit for tackling LCM problems of varying complexity. The broader applications of LCMs highlight its significance in diverse mathematical and real-world contexts. By mastering the concept of LCM, you unlock a key to solving a wide range of mathematical puzzles and practical problems. Remember to choose the method that best suits the numbers involved for efficiency and ease of calculation.
Latest Posts
Latest Posts
-
Points That Lie On The Same Line Are Collinear
Mar 28, 2025
-
Neutralizes Acidic Chyme Entering The Small Intestines
Mar 28, 2025
-
What Do Plants Store Glucose As
Mar 28, 2025
-
How Do You Find The Equation Of A Horizontal Line
Mar 28, 2025
-
What Is The Lcm Of 6 10 And 15
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 8 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
