Points That Lie On The Same Line Are Collinear
Juapaving
Mar 28, 2025 · 6 min read
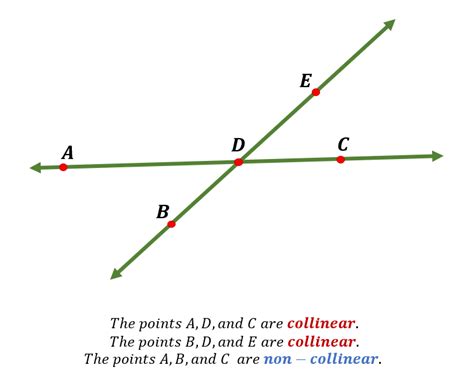
Table of Contents
Points That Lie on the Same Line Are Collinear: A Comprehensive Guide
Collinearity, a fundamental concept in geometry, refers to the property of points lying on the same straight line. Understanding collinearity is crucial for various mathematical applications, from basic geometry problems to advanced concepts in linear algebra and computer graphics. This comprehensive guide delves deep into the definition, properties, tests, and applications of collinear points.
Defining Collinearity: What Does it Mean?
In its simplest form, collinearity means that a set of points are situated on the same straight line. If three or more points are collinear, you can draw a single, perfectly straight line passing through all of them. This seemingly simple concept forms the basis for numerous geometrical theorems and problem-solving techniques. The absence of collinearity means the points form a non-linear configuration.
Visualizing Collinearity
Imagine three points, A, B, and C. If you can draw a straight line that passes through all three points without any deviation, then points A, B, and C are collinear. However, if you need to draw separate lines to connect each pair of points, then the points are not collinear. Consider the vertices of a triangle; these points are not collinear because they define a plane, not a line.
Determining Collinearity: Methods and Techniques
Several methods exist to determine whether a set of points are collinear. The choice of method often depends on the context and the information available.
1. Using the Slope Formula: A Simple Approach
For two points (x₁, y₁) and (x₂, y₂), the slope (m) of the line connecting them is calculated as:
m = (y₂ - y₁) / (x₂ - x₁)
If you have three or more points, and the slope between every pair of points is the same, then the points are collinear. This approach is straightforward but can be prone to errors if the points are close together or if there are many points to check. It's most effective for a small number of points.
Example: Consider the points A(1, 2), B(3, 4), and C(5, 6).
- Slope AB: (4 - 2) / (3 - 1) = 2 / 2 = 1
- Slope BC: (6 - 4) / (5 - 3) = 2 / 2 = 1
- Slope AC: (6 - 2) / (5 - 1) = 4 / 4 = 1
Since the slopes are all equal to 1, points A, B, and C are collinear.
2. Using the Area of a Triangle: A Geometric Approach
A more elegant and robust method involves calculating the area of the triangle formed by three points. If the area of the triangle is zero, then the three points are collinear. The area (A) of a triangle with vertices (x₁, y₁), (x₂, y₂), and (x₃, y₃) can be calculated using the determinant formula:
A = 0.5 * |x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)|
If A = 0, the points are collinear. This method is particularly useful when dealing with coordinates in a Cartesian plane.
Example: Let's use the same points A(1, 2), B(3, 4), and C(5, 6).
A = 0.5 * |1(4 - 6) + 3(6 - 2) + 5(2 - 4)| A = 0.5 * |-2 + 12 - 10| A = 0.5 * |0| A = 0
Since the area is 0, the points A, B, and C are collinear. This method neatly handles cases where the slope is undefined (vertical line).
3. Using Vectors: An Advanced Approach
Vector algebra provides another powerful method for determining collinearity. Three points are collinear if the vectors formed by connecting any two pairs of points are parallel. This means one vector is a scalar multiple of the other.
Example: Let's represent the points as vectors: A = <1, 2>, B = <3, 4>, C = <5, 6>.
- Vector AB = B - A = <2, 2>
- Vector BC = C - B = <2, 2>
- Vector AC = C - A = <4, 4>
Notice that AB = BC and AC = 2 * AB. Since AB and BC are equal and AC is a scalar multiple of AB, the vectors are parallel, and therefore the points A, B, and C are collinear.
Properties of Collinear Points
Understanding the properties of collinear points enhances problem-solving abilities in geometry. Some key properties include:
- Uniqueness of the Line: A unique straight line can pass through any two distinct points.
- Infinite Points: An infinite number of points can lie on a single straight line.
- Midpoint Theorem: If points A, B, and C are collinear, and B is the midpoint of AC, then AB = BC and AB + BC = AC.
- Ratio of Distances: If three points A, B, and C are collinear, the ratio of distances AB to BC is a constant.
Applications of Collinearity
Collinearity isn't just a theoretical concept; it finds practical applications in diverse fields:
1. Geometry and Trigonometry:
Collinearity is fundamental to many geometric theorems and proofs, such as Menelaus' Theorem and Ceva's Theorem, which deal with ratios of line segments in triangles. It plays a vital role in solving problems related to triangles, circles, and other geometric shapes. In trigonometry, collinearity aids in simplifying calculations involving angles and distances.
2. Computer Graphics:
In computer graphics and computer-aided design (CAD), collinearity is used to determine if points lie on the same line, a crucial element in rendering lines, polygons, and other geometric primitives. Algorithms for line clipping, polygon filling, and collision detection often rely on collinearity checks.
3. Linear Algebra:
In linear algebra, collinearity is related to the linear dependence of vectors. If vectors representing points are linearly dependent, then the points are collinear. This concept is pivotal in understanding concepts like vector spaces and linear transformations.
4. Spatial Reasoning and Physics:
Collinearity is important in understanding spatial relationships and modeling physical phenomena. For example, in physics, collinearity of forces simplifies the analysis of systems subject to multiple forces. Similarly, collinearity is essential in modeling projectile motion and other forms of motion analysis.
5. Surveying and Mapping:
Surveying and mapping techniques often rely on collinearity to ensure accurate measurements and representations of geographical features. Collinearity checks help validate data points and detect errors in surveying datasets.
Advanced Concepts and Extensions
Beyond the basic methods, more advanced techniques exist for determining collinearity, particularly when dealing with a large number of points or points in higher dimensions.
1. Collinearity in Higher Dimensions:
The concepts of collinearity extend beyond two-dimensional spaces. In three dimensions (and higher), collinearity refers to points lying on the same straight line within that higher-dimensional space. The methods for determining collinearity involve extending the vector approach and using concepts from linear algebra, such as linear dependence of vectors in higher-dimensional vector spaces.
2. Robust Collinearity Tests:
For real-world applications where data might contain noise or errors, robust collinearity tests are crucial. These techniques are designed to be less sensitive to outliers and small deviations from perfect collinearity. Methods like least-squares fitting and RANSAC (Random Sample Consensus) are frequently employed to handle noisy data in applications like image processing and computer vision.
Conclusion
Collinearity, while seemingly simple, is a powerful concept with far-reaching applications across various mathematical and computational fields. Understanding the different methods for determining collinearity and its properties is vital for solving geometric problems, creating efficient algorithms in computer graphics, and analyzing spatial relationships in diverse contexts. From basic slope calculations to advanced vector methods and robust statistical techniques, the choice of approach depends on the specific context and the characteristics of the data. Mastering this fundamental concept unlocks a deeper understanding of geometry and its applications in the real world.
Latest Posts
Latest Posts
-
35 Inches Is How Many Feet
Mar 31, 2025
-
3 Cm Is How Many Mm
Mar 31, 2025
-
How Many Lines Of Symmetry Are In A Star
Mar 31, 2025
-
Which Of The Following Is An Ecosystem
Mar 31, 2025
-
Least Common Multiple Of 20 And 50
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Points That Lie On The Same Line Are Collinear . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
