What Is The Lcm Of 6 10 And 15
Juapaving
Mar 28, 2025 · 5 min read
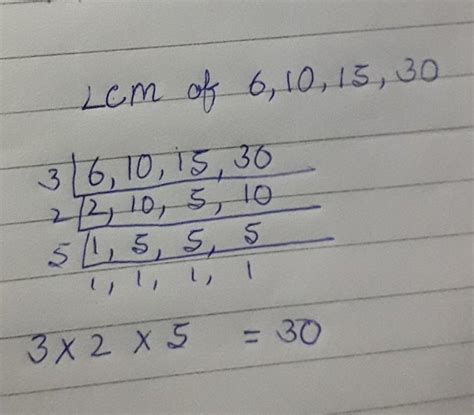
Table of Contents
What is the LCM of 6, 10, and 15? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, with applications ranging from simple fraction addition to complex scheduling problems. This article will comprehensively explore how to calculate the LCM of 6, 10, and 15, explaining the different methods and providing a deeper understanding of the underlying principles. We'll also touch upon the practical applications of LCMs and related concepts like the greatest common divisor (GCD).
Understanding Least Common Multiples (LCM)
Before diving into the calculation, let's solidify our understanding of LCMs. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers in the set. In simpler terms, it's the smallest number that all the numbers in the set can divide into without leaving a remainder.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12… and multiples of 3 are 3, 6, 9, 12, 15… The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The most straightforward method, particularly useful for smaller numbers, is to list the multiples of each number until a common multiple is found. Let's apply this to our numbers, 6, 10, and 15:
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66…
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70…
- Multiples of 15: 15, 30, 45, 60, 75…
Notice that 30 and 60 appear in all three lists. However, 30 is the smallest number common to all three lists. Therefore, the LCM of 6, 10, and 15 is 30.
This method is simple to understand but can become cumbersome and time-consuming when dealing with larger numbers or a greater number of integers.
Method 2: Prime Factorization
A more efficient and widely applicable method is using prime factorization. This method involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
- Prime Factorization of 6: 2 x 3
- Prime Factorization of 10: 2 x 5
- Prime Factorization of 15: 3 x 5
Now, to find the LCM, we consider the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Multiply these highest powers together: 2 x 3 x 5 = 30. Therefore, the LCM of 6, 10, and 15 is 30.
This method is significantly more efficient for larger numbers and is less prone to errors than the listing multiples method.
Method 3: Using the GCD (Greatest Common Divisor)
The LCM and GCD are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are two integers. This formula can be extended to more than two numbers, although it's slightly more complex. Let's find the GCD of 6, 10, and 15 first.
The GCD is the largest number that divides all three numbers without leaving a remainder. One way to find the GCD is by listing the divisors:
- Divisors of 6: 1, 2, 3, 6
- Divisors of 10: 1, 2, 5, 10
- Divisors of 15: 1, 3, 5, 15
The greatest common divisor among these lists is 1. Therefore, GCD(6, 10, 15) = 1.
While the formula above is directly applicable to two numbers, for more than two numbers, we often calculate the GCD pairwise and then work towards the overall GCD. In this case, we've already determined the GCD is 1.
However, using this method to calculate the LCM indirectly for multiple numbers is generally less efficient than prime factorization for more than two numbers.
Practical Applications of LCM
The concept of LCM finds its way into numerous real-world applications:
-
Scheduling: Imagine you have two machines that perform different tasks. Machine A completes a cycle every 6 minutes, and Machine B every 10 minutes. To determine when both machines will be at the starting point of their cycle simultaneously, you would calculate the LCM of 6 and 10 (which is 30). They will both be at the start of their cycles after 30 minutes.
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators. For example, to add 1/6 + 1/10 + 1/15, the LCM (30) becomes the common denominator, simplifying the calculation.
-
Project Management: In project management, LCM can help determine the synchronization points for various tasks with different durations.
-
Gear Ratios: In mechanical engineering, LCM is important in designing gear ratios to achieve desired speed and torque combinations.
-
Music Theory: The LCM is used in music theory to calculate the least common multiple of the note lengths to find the shortest time before a certain rhythmic pattern repeats.
-
Cyclic Events: Any situations involving repetitive events with different periods can use the LCM to find when the events will coincide. This includes natural phenomena, scheduling, and manufacturing processes.
Beyond the Basics: LCM and GCD for Larger Numbers
While the methods described above work well for smaller numbers, calculating the LCM for very large numbers can be computationally intensive. For such cases, more sophisticated algorithms, often leveraging the Euclidean algorithm for GCD calculation, are employed. These algorithms are implemented in mathematical software packages and programming languages to handle the complexities efficiently.
Conclusion
Finding the LCM of 6, 10, and 15, whether through listing multiples, prime factorization, or indirectly through the GCD, consistently yields the answer: 30. Understanding the different methods empowers you to choose the most efficient approach depending on the numbers involved. The concept of LCM extends far beyond basic arithmetic, playing a crucial role in various fields, highlighting its practical importance and relevance in a diverse range of applications. Mastering this concept strengthens your mathematical foundation and enhances your problem-solving skills across many disciplines.
Latest Posts
Latest Posts
-
Which Of The Following Is An Ecosystem
Mar 31, 2025
-
Least Common Multiple Of 20 And 50
Mar 31, 2025
-
List The Factors Of 100 That Are Prime
Mar 31, 2025
-
Do The Diagonals Of A Kite Bisect Teachother
Mar 31, 2025
-
What Is The Factor Of 71
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 6 10 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
