How Do You Find The Equation Of A Horizontal Line
Juapaving
Mar 28, 2025 · 6 min read
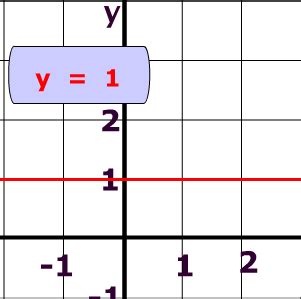
Table of Contents
How Do You Find the Equation of a Horizontal Line? A Comprehensive Guide
Understanding the equation of a horizontal line is fundamental to grasping core concepts in algebra and coordinate geometry. This comprehensive guide will delve deep into the topic, exploring not only the equation itself but also its implications, applications, and how it relates to other mathematical concepts. We’ll cover everything from the basics to more advanced considerations, ensuring a thorough understanding for students of all levels.
Understanding the Cartesian Coordinate System
Before diving into the equation of a horizontal line, let's establish a firm grasp of the Cartesian coordinate system. This system uses two perpendicular number lines, the x-axis (horizontal) and the y-axis (vertical), to define points in a plane. Each point is uniquely identified by its coordinates (x, y), representing its horizontal and vertical distance from the origin (0, 0).
Key Features of the Cartesian Plane:
- Origin: The point where the x and y axes intersect (0, 0).
- X-axis: The horizontal line representing the independent variable.
- Y-axis: The vertical line representing the dependent variable.
- Quadrants: The four regions created by the intersection of the x and y axes.
Defining a Horizontal Line
A horizontal line is a straight line that runs parallel to the x-axis. This means that every point on a horizontal line shares the same y-coordinate. No matter how far along the x-axis you move, the y-value remains constant. This constancy is the key to understanding its equation.
Deriving the Equation of a Horizontal Line
Because every point on a horizontal line has the same y-coordinate, the equation of a horizontal line is remarkably simple:
y = k
Where 'k' is a constant representing the y-coordinate of every point on the line. This constant can be any real number, positive, negative, or zero.
Examples:
- y = 3: This represents a horizontal line passing through all points with a y-coordinate of 3, such as (1, 3), (0, 3), (-2, 3), and so on.
- y = -2: This represents a horizontal line passing through all points with a y-coordinate of -2, such as (5, -2), (-3, -2), (0, -2), etc.
- y = 0: This is a special case, representing the x-axis itself. All points on the x-axis have a y-coordinate of 0.
Visualizing Horizontal Lines
Imagine graphing these equations. For y = 3, you would plot points (1, 3), (2, 3), (3, 3), and so on. Connecting these points will produce a perfectly straight horizontal line parallel to the x-axis and three units above it. Similarly, for y = -2, the line will be parallel to the x-axis and two units below it.
Distinguishing Horizontal Lines from Vertical Lines
It's crucial to distinguish horizontal lines from vertical lines. While a horizontal line has a constant y-coordinate, a vertical line has a constant x-coordinate. The equation of a vertical line is:
x = c
Where 'c' is a constant representing the x-coordinate of every point on the line.
Applications of Horizontal Lines
Horizontal lines find numerous applications across various fields, including:
1. Graphing and Data Representation:
Horizontal lines are frequently used in graphs to represent constant values or thresholds. For instance, in a line graph showing temperature over time, a horizontal line might indicate a constant temperature throughout a period.
2. Geometry and Trigonometry:
In geometry, horizontal lines are used to define parallel lines and to construct geometric shapes. In trigonometry, the x-axis is a horizontal line serving as a reference for angles.
3. Linear Equations and Systems of Equations:
Understanding horizontal lines is essential when solving systems of linear equations. A system involving a horizontal line and a non-horizontal line will have exactly one solution (the intersection point). A system involving two parallel horizontal lines will have no solution.
4. Calculus and Limits:
In calculus, horizontal lines are important in finding horizontal asymptotes of functions. A horizontal asymptote represents the value that a function approaches as the independent variable approaches infinity or negative infinity.
5. Computer Graphics and Game Development:
In computer graphics and game development, horizontal lines are used to define boundaries, create level geometry, and define elements of the user interface.
Solving Problems Involving Horizontal Lines
Let's work through some examples to solidify our understanding:
Example 1: Find the equation of the horizontal line passing through the point (4, -5).
Since it's a horizontal line, the y-coordinate remains constant. The y-coordinate of the given point is -5. Therefore, the equation of the line is:
y = -5
Example 2: Determine if the points (2, 7) and (5, 7) lie on the same horizontal line.
Both points have the same y-coordinate, which is 7. Therefore, they both lie on the horizontal line y = 7.
Example 3: Find the intersection point of the horizontal line y = 2 and the line y = x + 1.
Substitute y = 2 into the equation y = x + 1:
2 = x + 1
Solving for x, we get x = 1. Therefore, the intersection point is (1, 2).
Advanced Concepts and Further Exploration
While the equation of a horizontal line (y = k) is straightforward, its understanding opens doors to more complex concepts:
1. Slope of a Horizontal Line:
The slope of a line represents its steepness. The slope of a horizontal line is always zero (0). This is because there's no vertical change (Δy = 0) for any horizontal change (Δx). The slope formula, m = Δy/Δx, results in 0/Δx = 0.
2. Parallel and Perpendicular Lines:
Two horizontal lines are always parallel to each other because they have the same slope (0). A horizontal line is perpendicular to a vertical line, as they intersect at a right angle.
3. Linear Transformations:
Horizontal lines can be transformed through various linear transformations such as translations (shifting), scaling, and rotations. Understanding how these transformations affect the equation of the line is crucial in linear algebra and computer graphics.
Conclusion: Mastering the Equation of a Horizontal Line
The equation of a horizontal line, y = k, though simple in form, is a fundamental building block in mathematics and numerous applications. By understanding its derivation, properties, and applications, you'll build a solid foundation for more advanced mathematical concepts and problem-solving skills. This comprehensive guide has equipped you with the knowledge to confidently identify, analyze, and utilize horizontal lines in various contexts. Remember to practice regularly to solidify your understanding and prepare yourself for more intricate mathematical challenges.
Latest Posts
Latest Posts
-
35 Inches Is How Many Feet
Mar 31, 2025
-
3 Cm Is How Many Mm
Mar 31, 2025
-
How Many Lines Of Symmetry Are In A Star
Mar 31, 2025
-
Which Of The Following Is An Ecosystem
Mar 31, 2025
-
Least Common Multiple Of 20 And 50
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Do You Find The Equation Of A Horizontal Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
