What Is The Factor Of 71
Juapaving
Mar 31, 2025 · 5 min read
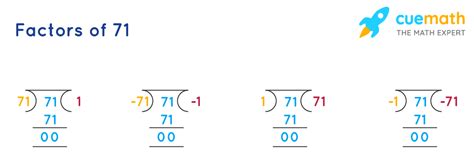
Table of Contents
What is the Factor of 71? A Deep Dive into Prime Numbers and Factorization
The question, "What is the factor of 71?" might seem deceptively simple. However, exploring this seemingly straightforward query opens the door to a deeper understanding of number theory, prime numbers, and the fundamental processes of factorization. This article will not only answer the question directly but also delve into the broader context of prime numbers and their significance in mathematics.
Understanding Factors
Before we tackle the specific case of 71, let's establish a clear understanding of what a factor is. In mathematics, a factor (or divisor) of a number is a whole number that divides that number exactly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 evenly.
Finding the factors of a number is a fundamental operation in arithmetic and forms the basis for many more advanced mathematical concepts. The process of finding all factors is often referred to as factorization.
Identifying Prime Numbers
The key to understanding the factors of 71 lies in the concept of prime numbers. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In simpler terms, a prime number is only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on.
Prime numbers are considered the "building blocks" of all other natural numbers. This is because every natural number greater than 1 can be expressed as a unique product of prime numbers (this is known as the Fundamental Theorem of Arithmetic). This unique representation is crucial in various mathematical fields, including cryptography and computer science.
Determining the Factors of 71
Now, let's return to our original question: What are the factors of 71? To determine this, we need to check if 71 is divisible by any smaller numbers. We can start by checking the smallest prime numbers:
- Divisibility by 2: 71 is not an even number, so it's not divisible by 2.
- Divisibility by 3: The sum of the digits of 71 is 7 + 1 = 8, which is not divisible by 3. Therefore, 71 is not divisible by 3.
- Divisibility by 5: 71 does not end in 0 or 5, so it's not divisible by 5.
- Divisibility by 7: 71 divided by 7 is approximately 10.14, indicating it's not divisible by 7.
- Divisibility by 11: 71 divided by 11 is approximately 6.45, indicating it's not divisible by 11.
We could continue checking divisibility by other prime numbers, but notice a pattern emerging. Since the square root of 71 is approximately 8.4, we only need to check prime numbers up to 7. After checking primes up to 7, we find that 71 is not divisible by any smaller number.
Therefore, the only factors of 71 are 1 and 71 itself. This confirms that 71 is a prime number.
The Significance of Prime Numbers
The fact that 71 is a prime number is not just a trivial observation. Prime numbers hold immense significance in various branches of mathematics and computer science:
1. Fundamental Theorem of Arithmetic:
As mentioned earlier, the Fundamental Theorem of Arithmetic states that every integer greater than 1 can be uniquely represented as a product of prime numbers. This theorem is foundational to many areas of number theory.
2. Cryptography:
Prime numbers play a crucial role in modern cryptography. Many encryption algorithms rely on the difficulty of factoring very large numbers into their prime factors. The security of these algorithms depends on the computational infeasibility of factoring these large numbers, even with powerful computers.
3. Number Theory Research:
Prime numbers are a central topic of ongoing research in number theory. Many unsolved problems in mathematics, such as the Riemann Hypothesis, are related to the distribution and properties of prime numbers.
4. Computer Science:
Prime numbers are used in hash table algorithms, pseudorandom number generators, and other areas of computer science. Their unique properties make them ideal for various computational tasks.
Advanced Concepts Related to Prime Factorization
While finding the factors of 71 was relatively straightforward, factorization becomes significantly more complex with larger numbers. Various algorithms have been developed to efficiently factor large numbers, including:
- Trial Division: A simple but inefficient method for finding factors by testing divisibility with successively larger prime numbers.
- Pollard's Rho Algorithm: A probabilistic algorithm that is relatively efficient for finding small prime factors.
- General Number Field Sieve (GNFS): The most efficient known algorithm for factoring very large numbers. This algorithm is used to break cryptographic systems based on the difficulty of factorization.
These algorithms highlight the computational complexity associated with prime factorization, even with the assistance of powerful computers.
Applications of Factorization Beyond Prime Numbers
The concept of factorization extends beyond just identifying prime factors. It's a fundamental operation used in various mathematical applications:
- Simplifying fractions: Factorization helps to simplify fractions by identifying common factors in the numerator and denominator.
- Solving polynomial equations: Factorization plays a crucial role in solving polynomial equations by breaking down complex expressions into simpler factors.
- Algebraic manipulations: Factorization is an essential tool for manipulating algebraic expressions, simplifying calculations, and solving equations.
Conclusion: The Importance of Understanding Factors and Prime Numbers
The seemingly simple question, "What is the factor of 71?", has led us on a journey into the fascinating world of prime numbers and factorization. We've established that the factors of 71 are 1 and 71, confirming its status as a prime number. However, the significance of this finding extends far beyond this specific example. Prime numbers are fundamental building blocks of mathematics, critical to cryptography, and the subject of ongoing mathematical research. Understanding factorization and prime numbers is not just an academic exercise; it's a cornerstone of many important areas of mathematics and computer science. The exploration of prime numbers and their properties continues to reveal intriguing insights into the fundamental nature of numbers and their interrelationships. The seemingly simple concept hides a wealth of complexity and profound implications, highlighting the beauty and depth of mathematical exploration. The pursuit of understanding the factors of numbers, even seemingly simple ones like 71, underscores the enduring power and relevance of mathematical inquiry.
Latest Posts
Latest Posts
-
15 4 As A Mixed Number
Apr 01, 2025
-
What Organelle Is The Site Of Aerobic Respiration
Apr 01, 2025
-
1 5 Gallons Is How Many Liters
Apr 01, 2025
-
How To Turn Gas Into Liquid
Apr 01, 2025
-
What Are The Kinds Of Motion
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Factor Of 71 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
