Do The Diagonals Of A Kite Bisect Teachother
Juapaving
Mar 31, 2025 · 5 min read
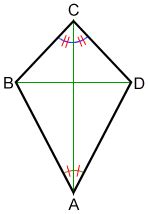
Table of Contents
Do the Diagonals of a Kite Bisect Each Other? Exploring the Geometry of Kites
The question of whether the diagonals of a kite bisect each other is a fundamental concept in geometry, particularly when studying quadrilaterals. Understanding this property requires a thorough exploration of the kite's defining characteristics and the relationships between its sides and diagonals. This article will delve into the geometry of kites, proving whether or not the diagonals bisect each other, and exploring related theorems and properties.
Defining a Kite: A Geometric Shape
A kite is a quadrilateral with two pairs of adjacent sides that are congruent (equal in length). This means that two sides are equal, and the other two sides are also equal, but the equal pairs are adjacent to each other, not opposite. This definition sets the kite apart from other quadrilaterals like parallelograms, rectangles, and rhombuses.
It's crucial to distinguish between the properties of a kite and those of other quadrilaterals. For instance, a rhombus is a kite where all four sides are congruent. A square is a special case of a kite (and a rhombus) where all four sides are congruent and all four angles are right angles. However, a general kite doesn't necessarily possess these additional characteristics.
Let's visualize a kite. Imagine a classic children's kite – its shape perfectly embodies the definition. The two shorter sides meet at a point, forming one pair of adjacent congruent sides. Similarly, the two longer sides meet at the other point, forming the second pair of adjacent congruent sides. The diagonals of the kite connect opposite vertices.
Investigating the Diagonals: Do They Bisect Each Other?
The key question we're addressing is whether the diagonals of a kite bisect each other. Bisecting means dividing something into two equal parts. In the context of a kite, if the diagonals bisect each other, it means they intersect at a point such that the point divides each diagonal into two equal segments.
The answer is: no, the diagonals of a kite do not necessarily bisect each other. This is a crucial distinction between kites and other quadrilaterals like rectangles and rhombuses. While the diagonals of a rectangle and a rhombus do bisect each other, the same cannot be said for a general kite.
Proof: Demonstrating the Non-Bisecting Property
Let's consider a kite ABCD, where AB = AD and BC = CD. Let the diagonals AC and BD intersect at point O.
To prove that the diagonals don't necessarily bisect each other, we need to demonstrate a scenario where AO ≠ OC and BO ≠ OD. We can do this through a counterexample.
Imagine a kite where AB = AD = 2 units and BC = CD = 4 units. You can draw this kite; you'll quickly notice that the diagonal AC will be longer than the diagonal BD. Furthermore, the intersection point O will not divide the diagonals into equal halves. AO will be different from OC, and BO will be different from OD. This demonstrates that the diagonals of a kite, in general, do not bisect each other.
The One Exception: The Rhombus-Kite Relationship
However, there is a significant exception. If the kite is also a rhombus (meaning all four sides are equal), then its diagonals do bisect each other. This is because a rhombus is a special case of a kite with additional properties. In a rhombus, the diagonals are perpendicular bisectors of each other. This means they intersect at right angles and divide each other into two equal segments.
This reinforces the importance of the precise definition of a kite. The properties of the diagonals are directly linked to the properties of the sides.
Exploring Other Properties of Kites
While the diagonals of a kite don't generally bisect each other, they possess other interesting properties:
1. One Diagonal Bisects the Other:
One diagonal of a kite always bisects the other. Specifically, the diagonal connecting the vertices with unequal adjacent sides (the longer diagonal) bisects the diagonal connecting the vertices with equal adjacent sides (the shorter diagonal). This bisecting property holds true even when the kite is not a rhombus.
2. Perpendicular Diagonals:
The diagonals of a kite are always perpendicular to each other. This means they intersect at a right angle (90 degrees). This perpendicularity is a key characteristic of kites, irrespective of whether the diagonals bisect each other.
3. Area of a Kite:
The area of a kite can be easily calculated using its diagonals. The formula is:
Area = (1/2) * d1 * d2
where d1 and d2 are the lengths of the two diagonals.
This formula highlights the importance of the diagonals in determining the kite's area.
Applications of Kite Geometry: Real-world Examples
Understanding the geometry of kites is not just an abstract mathematical exercise; it has practical applications:
-
Engineering and Design: Kite shapes appear in various engineering designs, from architectural structures to certain types of bridges. Knowing the properties of diagonals is essential for structural stability calculations.
-
Computer Graphics and Animation: The kite shape is used in computer graphics and animation to create specific shapes and patterns. Understanding its geometrical properties is crucial for achieving precise visual effects.
-
Art and Design: The symmetry and unique properties of kites make it a popular shape in various art forms, from paintings to fabric designs.
-
Nature: Kite-like shapes can be observed in certain natural formations and the arrangement of elements in nature, demonstrating the mathematical principles at play in the natural world.
Conclusion: A Deeper Understanding of Quadrilaterals
The question of whether the diagonals of a kite bisect each other highlights the importance of precise definitions and the subtle differences between various quadrilaterals. While the diagonals of a kite do not generally bisect each other, they are always perpendicular, and one diagonal always bisects the other. This property, combined with other characteristics, makes kites a fascinating subject of study within geometry, with implications extending beyond the classroom into real-world applications. Understanding these properties allows for a more comprehensive understanding of geometric shapes and their diverse characteristics. Remembering that a rhombus is a special case of a kite where all sides are equal helps clarify the exceptions to the general rule concerning diagonal bisection. This careful distinction is essential for accurate geometric reasoning and problem-solving.
Latest Posts
Latest Posts
-
35 Degrees C Is What In Fahrenheit
Apr 01, 2025
-
What Is A Good Conductor Of Heat And Electrocty
Apr 01, 2025
-
Equation Of Line Parallel To X Axis
Apr 01, 2025
-
A Chemical Equation Is Balanced When
Apr 01, 2025
-
Cold B Lood Vs Cold Heart
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Do The Diagonals Of A Kite Bisect Teachother . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
