List The Factors Of 100 That Are Prime
Juapaving
Mar 31, 2025 · 5 min read
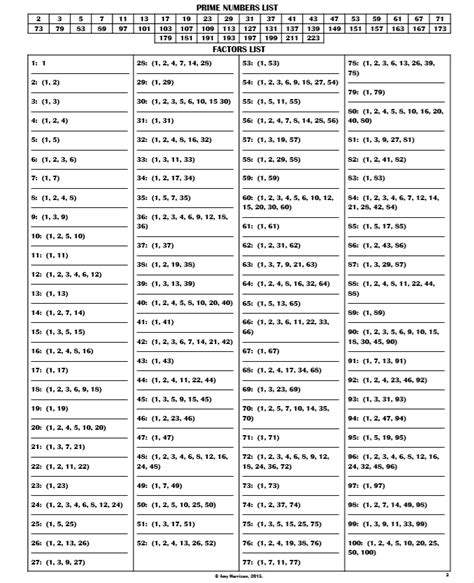
Table of Contents
Listing the Prime Factors of 100: A Deep Dive into Number Theory
The seemingly simple question, "What are the prime factors of 100?" opens a door to a fascinating exploration of number theory, a branch of mathematics with implications far beyond basic arithmetic. Understanding prime factorization is fundamental to various mathematical concepts and has practical applications in cryptography and computer science. This article will not only answer the question directly but delve deeper into the concepts of prime numbers, factorization, and their significance.
What are Prime Numbers?
Before we tackle the prime factors of 100, let's define what a prime number is. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In simpler terms, a prime number is only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered prime, and 2 is the only even prime number.
The fundamental theorem of arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors). This unique factorization is crucial to many areas of mathematics.
Finding the Prime Factors of 100
Now, let's find the prime factors of 100. We can do this through a process called prime factorization. There are several methods to achieve this, but here's a common approach:
-
Start with the smallest prime number, 2: Is 100 divisible by 2? Yes, 100 ÷ 2 = 50.
-
Continue with the result: Now we consider 50. Is 50 divisible by 2? Yes, 50 ÷ 2 = 25.
-
Keep going: Now we have 25. Is 25 divisible by 2? No. Let's try the next prime number, 3. Is 25 divisible by 3? No. Let's try 5. Is 25 divisible by 5? Yes, 25 ÷ 5 = 5.
-
The final prime factor: We're left with 5, which is itself a prime number.
Therefore, the prime factorization of 100 is 2 x 2 x 5 x 5, or 2² x 5². This means the prime factors of 100 are 2 and 5.
Visualizing Prime Factorization: Factor Trees
A helpful visual tool for prime factorization is the factor tree. Let's create one for 100:
100
/ \
2 50
/ \
2 25
/ \
5 5
The factor tree branches down until all the leaves are prime numbers. This clearly shows that the prime factors of 100 are 2 and 5.
The Significance of Prime Factorization
The seemingly simple act of finding the prime factors of a number has profound implications in several areas:
1. Cryptography
Prime numbers form the bedrock of modern cryptography. Many encryption algorithms, such as RSA (Rivest-Shamir-Adleman), rely on the difficulty of factoring large numbers into their prime components. The security of these systems depends on the fact that while multiplying two large prime numbers is relatively easy, factoring their product back into the original primes is computationally extremely difficult.
2. Computer Science
Prime numbers play a crucial role in various aspects of computer science, including:
- Hashing: Prime numbers are often used in hash table algorithms to minimize collisions and improve efficiency.
- Random Number Generation: Prime numbers are integral to creating robust and unpredictable random number generators.
- Data Structures: Certain data structures, such as sieve algorithms for finding primes, leverage prime number properties.
3. Number Theory and Abstract Algebra
Prime factorization is a fundamental concept in number theory, underpinning many theorems and proofs. It's essential for understanding concepts like modular arithmetic, congruences, and other advanced mathematical ideas. The unique factorization property is a cornerstone of abstract algebra, providing structure and allowing for generalizations to more abstract mathematical systems.
Beyond 100: Exploring Prime Factorization of Other Numbers
Let's extend our understanding by examining the prime factorization of a few other numbers:
- 12: 12 = 2 x 2 x 3 = 2² x 3
- 24: 24 = 2 x 2 x 2 x 3 = 2³ x 3
- 36: 36 = 2 x 2 x 3 x 3 = 2² x 3²
- 1000: 1000 = 2 x 2 x 2 x 5 x 5 x 5 = 2³ x 5³
Notice how different numbers have different combinations of prime factors. The fundamental theorem of arithmetic guarantees that this factorization is unique for each number.
Advanced Concepts Related to Prime Numbers
Let's briefly touch upon some more advanced concepts related to prime numbers:
- Infinitude of Primes: Euclid's proof demonstrates that there are infinitely many prime numbers. This means there is no largest prime number.
- Prime Number Theorem: This theorem provides an estimate of the distribution of prime numbers. While not providing an exact formula, it gives a good approximation of how many primes exist below a given number.
- Twin Primes: These are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13). The Twin Prime Conjecture proposes that there are infinitely many twin primes, but this remains unproven.
- Mersenne Primes: These are prime numbers of the form 2<sup>p</sup> - 1, where 'p' is also a prime number. The largest known prime numbers are often Mersenne primes.
Conclusion: The Enduring Importance of Prime Numbers
The prime factors of 100 – 2 and 5 – may seem like a simple answer, but the journey to arrive at this answer opens a gateway to a rich and complex world of mathematics. The concept of prime factorization, seemingly straightforward, underpins fundamental aspects of cryptography, computer science, and number theory. Understanding prime numbers and their properties is crucial for anyone interested in exploring the deeper realms of mathematics and its practical applications in the modern world. From securing online transactions to optimizing computer algorithms, prime numbers remain an active area of research and continue to shape the digital landscape we live in. The seemingly simple question about the prime factors of 100 has led us on a fascinating exploration into a fundamental concept with far-reaching consequences.
Latest Posts
Latest Posts
-
A Chemical Equation Is Balanced When
Apr 01, 2025
-
Cold B Lood Vs Cold Heart
Apr 01, 2025
-
Lowest Common Denominator Of 12 And 9
Apr 01, 2025
-
What Is The Advantage Of A Four Chambered Heart
Apr 01, 2025
-
Endocrine Glands Are Often Called Ducted Glands True False
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about List The Factors Of 100 That Are Prime . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
