What Is The Lcm Of 2 And 8
Juapaving
Mar 28, 2025 · 5 min read
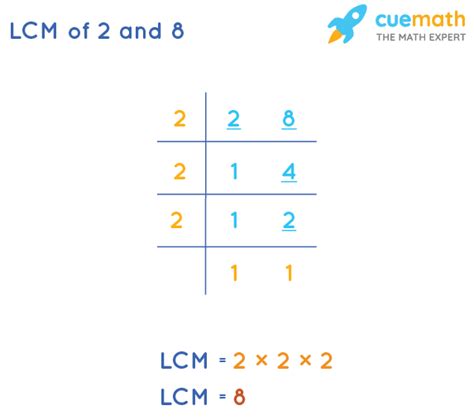
Table of Contents
What is the LCM of 2 and 8? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, algebra, and even advanced number theory. This article will explore the question, "What is the LCM of 2 and 8?", not just by providing the answer, but by delving into the various methods for calculating the LCM, explaining the underlying principles, and showcasing its practical applications. We'll cover different approaches, from listing multiples to using prime factorization and the greatest common divisor (GCD), ensuring a comprehensive understanding for readers of all levels.
Understanding Least Common Multiples (LCM)
Before jumping into the specifics of finding the LCM of 2 and 8, let's establish a clear understanding of what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the integers as factors.
For example, consider the numbers 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20, 24... and the multiples of 6 are 6, 12, 18, 24, 30... Notice that 12 and 24 are common multiples of both 4 and 6. However, 12 is the smallest common multiple, making it the least common multiple (LCM) of 4 and 6.
Method 1: Listing Multiples
The most straightforward method for finding the LCM, especially for smaller numbers, is by listing the multiples of each number until a common multiple is found. Let's apply this method to find the LCM of 2 and 8:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 8: 8, 16, 24, 32, 40...
By comparing the lists, we can see that 8 is the smallest number that appears in both lists. Therefore, the LCM of 2 and 8 is 8.
This method is simple and intuitive, but it becomes less efficient when dealing with larger numbers or a greater number of integers. Imagine trying to find the LCM of 24 and 36 using this method – the lists would get quite long!
Method 2: Prime Factorization
A more efficient and systematic approach is to use prime factorization. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves). This method is particularly useful for larger numbers.
Let's find the LCM of 2 and 8 using prime factorization:
-
Find the prime factorization of each number:
- 2 = 2¹
- 8 = 2³
-
Identify the highest power of each prime factor present in the factorizations:
- The only prime factor is 2, and the highest power is 2³.
-
Multiply the highest powers of all prime factors together:
- LCM(2, 8) = 2³ = 8
Therefore, the LCM of 2 and 8 is 8. This method is more efficient and scalable than simply listing multiples, making it preferable for larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are intimately related. There's a handy formula that connects them:
LCM(a, b) * GCD(a, b) = a * b
Where 'a' and 'b' are the two integers.
Let's use this formula to find the LCM of 2 and 8:
-
Find the GCD of 2 and 8: The greatest common divisor of 2 and 8 is 2 (as 2 is the largest number that divides both 2 and 8).
-
Apply the formula:
- LCM(2, 8) * GCD(2, 8) = 2 * 8
- LCM(2, 8) * 2 = 16
- LCM(2, 8) = 16 / 2 = 8
Therefore, the LCM of 2 and 8 is 8. This method provides an alternative approach, leveraging the relationship between LCM and GCD. Finding the GCD can be done efficiently using the Euclidean algorithm, especially for larger numbers.
Practical Applications of LCM
Understanding and calculating LCMs isn't just an academic exercise; it has numerous practical applications in various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators. This ensures that the fractions are expressed with equivalent parts for accurate calculations.
-
Scheduling and Planning: LCMs are useful in scheduling events that occur at different intervals. For example, if event A happens every 2 days and event B happens every 8 days, the LCM (8) tells us that both events will occur together every 8 days.
-
Gear Ratios and Mechanical Engineering: In mechanical systems, gear ratios and rotational speeds are often related by LCMs. Calculating the LCM helps engineers design systems with synchronized movement.
-
Music Theory: In music, LCMs help determine the least common multiple of note durations, which is crucial for understanding rhythmic patterns and composition.
-
Computer Science: LCMs play a role in various algorithms and data structures in computer science, impacting the efficiency and performance of software.
Advanced Concepts and Extensions
While we've focused on finding the LCM of two numbers, the concept extends to finding the LCM of more than two numbers. The principles remain the same; you can use prime factorization or adapt the methods described above to handle multiple integers.
Furthermore, the concept of LCM can be extended to other mathematical structures, such as polynomials. Finding the LCM of polynomials involves similar techniques, but instead of prime factors, we work with irreducible polynomials.
Conclusion
Finding the LCM of 2 and 8, as demonstrated through multiple methods, highlights the fundamental importance of this concept in mathematics and its practical applications across various disciplines. The choice of method depends on the complexity of the numbers involved and the context of the problem. Whether you use the simple method of listing multiples, the efficient prime factorization approach, or the formula involving the GCD, the answer remains the same: the LCM of 2 and 8 is 8. This seemingly simple calculation underscores a powerful mathematical tool with far-reaching consequences. Understanding LCMs is a cornerstone of mathematical literacy, equipping you with the skills to solve a wide range of problems efficiently and accurately.
Latest Posts
Latest Posts
-
Which Are The Most Abundant Gases In The Atmosphere
Mar 31, 2025
-
What Are Three Examples Of A Chemical Change
Mar 31, 2025
-
What Is Prime Factors Of 24
Mar 31, 2025
-
Notes On Newtons Laws Of Motion
Mar 31, 2025
-
How Many Bonds Does Sulfur Have
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 2 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
