What Is Prime Factors Of 24
Juapaving
Mar 31, 2025 · 5 min read
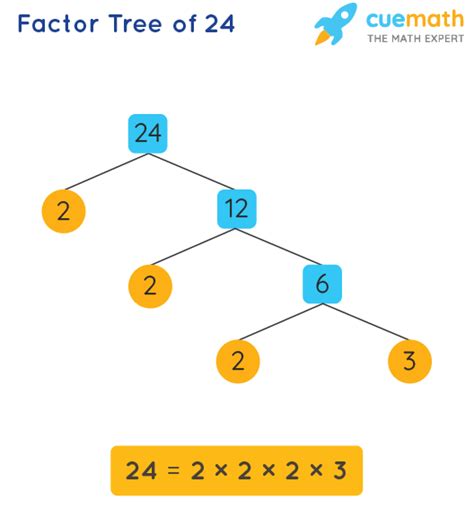
Table of Contents
What are the Prime Factors of 24? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple task, especially for a small number like 24. However, understanding the process and its implications goes far beyond just getting the answer. This article will delve deep into determining the prime factors of 24, explaining the underlying concepts of prime numbers, prime factorization, and its applications in various fields of mathematics and beyond. We'll also explore some advanced concepts related to prime factorization.
Understanding Prime Numbers
Before we tackle the prime factors of 24, let's establish a solid understanding of what a prime number is. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means it's not divisible by any other whole number without leaving a remainder. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number.
Key Characteristics of Prime Numbers:
- Divisibility: Only divisible by 1 and itself.
- Infinitude: There are infinitely many prime numbers. This is a fundamental theorem in number theory.
- Distribution: While the distribution of primes is irregular, there are patterns and conjectures about their spacing. The Prime Number Theorem provides an approximation of the density of primes.
Prime Factorization: Breaking Down Numbers
Prime factorization is the process of expressing a composite number (a number greater than 1 that is not prime) as a product of its prime factors. Every composite number can be uniquely expressed as a product of primes. This is known as the Fundamental Theorem of Arithmetic. This unique representation is crucial in many mathematical applications.
For example, let's consider the number 12. Its prime factorization is 2 x 2 x 3 (or 2² x 3). This means 12 can be built solely by multiplying the prime numbers 2 and 3. No other combination of primes will produce 12.
Finding the Prime Factors of 24: A Step-by-Step Approach
Now, let's determine the prime factors of 24. We can use a method called the factor tree.
-
Start with the number: Begin with the number 24.
-
Find the smallest prime factor: The smallest prime number is 2. 24 is divisible by 2 (24 ÷ 2 = 12). So, we write 24 as 2 x 12.
-
Continue factoring: Now, we factor 12. The smallest prime factor of 12 is also 2 (12 ÷ 2 = 6). So, we have 2 x 2 x 6.
-
Keep going until all factors are prime: Next, we factor 6. The smallest prime factor of 6 is 2 (6 ÷ 2 = 3). This gives us 2 x 2 x 2 x 3.
-
Identify the prime factors: All the factors are now prime numbers (2 and 3). Therefore, the prime factorization of 24 is 2 x 2 x 2 x 3, or 2³ x 3.
Visualizing the Factor Tree for 24
A factor tree provides a visual representation of this process:
24
/ \
2 12
/ \
2 6
/ \
2 3
This tree clearly shows that the prime factors of 24 are 2 (three times) and 3 (once).
Applications of Prime Factorization
Prime factorization might seem like a simple mathematical exercise, but it has profound implications in various fields:
-
Cryptography: Prime factorization forms the basis of many modern encryption algorithms, such as RSA. The difficulty of factoring very large numbers into their prime components is what makes these encryption methods secure.
-
Number Theory: Prime factorization is fundamental to many areas of number theory, including the study of modular arithmetic, Diophantine equations, and the distribution of prime numbers.
-
Computer Science: Algorithms for prime factorization are constantly being refined and improved. Their efficiency has implications for various computational tasks.
-
Coding Theory: Prime numbers play a crucial role in error-correcting codes, which are used to ensure data integrity in various communication systems.
-
Abstract Algebra: Prime factorization concepts extend to more abstract algebraic structures, such as rings and fields.
Beyond the Basics: Exploring Advanced Concepts
Let's briefly touch upon some more advanced concepts related to prime factorization:
-
Greatest Common Divisor (GCD): Finding the GCD of two or more numbers involves using their prime factorizations. The GCD is the product of the common prime factors raised to the lowest power. For example, the GCD of 24 (2³ x 3) and 36 (2² x 3²) is 2² x 3 = 12.
-
Least Common Multiple (LCM): Similarly, finding the LCM utilizes prime factorizations. The LCM is the product of all prime factors raised to the highest power. The LCM of 24 and 36 is 2³ x 3² = 72.
-
Modular Arithmetic: Prime factorization is essential in modular arithmetic, which involves operations on remainders after division. This has applications in cryptography and other areas.
Conclusion: The Significance of Prime Factors
The seemingly simple task of finding the prime factors of 24 – 2³ x 3 – opens a door to a vast and fascinating world of mathematical concepts. Understanding prime numbers and prime factorization is not just about solving arithmetic problems; it's about grasping fundamental principles that underpin many crucial areas of mathematics, computer science, and cryptography. The unique factorization property ensures a solid foundation for more advanced mathematical explorations. From the seemingly simple to the incredibly complex, the prime factors of a number hold a significant place in the realm of mathematics and beyond. The more you delve into this topic, the more you’ll appreciate the elegant simplicity and profound depth of prime factorization.
Latest Posts
Latest Posts
-
How Do You Factorize An Equation
Apr 02, 2025
-
Can Triangle Have 2 Right Angles
Apr 02, 2025
-
Common Factors Of 20 And 25
Apr 02, 2025
-
What Is A Negative Rational Number
Apr 02, 2025
-
According To The Fluid Mosaic Model Of The Cell Membrane
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is Prime Factors Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
