What Is The Difference Between Surface Area And Area
Juapaving
Mar 28, 2025 · 6 min read
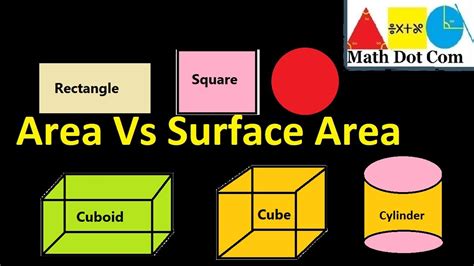
Table of Contents
What's the Difference Between Surface Area and Area? A Deep Dive
Understanding the difference between surface area and area is crucial in various fields, from basic geometry to advanced engineering and architecture. While both concepts relate to the measurement of space, they apply to different dimensional aspects of objects. This comprehensive guide will delve deep into the nuances of surface area and area, exploring their definitions, calculations, and practical applications. We'll also look at how these concepts relate to volume and explore some common misconceptions.
Defining Area: Two-Dimensional Measurement
Area refers to the two-dimensional space occupied by a flat shape or the surface of a three-dimensional object. It quantifies the amount of surface enclosed within a given boundary. Think of it as the amount of paint needed to cover a flat surface completely.
The units of area are always squared units, such as square meters (m²), square feet (ft²), square centimeters (cm²), etc. This is because area represents a two-dimensional quantity – length multiplied by width.
Calculating Area: The methods for calculating area vary depending on the shape:
- Rectangle: Area = length × width
- Square: Area = side × side (side²)
- Triangle: Area = (1/2) × base × height
- Circle: Area = π × radius²
- Irregular Shapes: For irregular shapes, techniques like dividing the shape into smaller, regular shapes or using calculus (integration) are often employed.
Examples of Area in Everyday Life:
- Calculating the size of a room: To determine the amount of flooring or carpeting needed, you'd calculate the area of the room.
- Landscaping: Determining the amount of grass seed or fertilizer required for a lawn involves calculating its area.
- Painting a wall: The area of the wall dictates the amount of paint needed for a single coat.
- Sewing: Calculating the area of fabric needed for a garment involves understanding area measurements.
Defining Surface Area: Three-Dimensional Measurement
Surface area, on the other hand, refers to the total area of all the faces or surfaces of a three-dimensional object. It measures the total external area of a solid figure. Imagine wrapping a present – the amount of wrapping paper needed is directly related to the surface area of the gift.
Surface area is also measured in squared units, reflecting its two-dimensional nature. However, it's applied to the external surfaces of three-dimensional objects.
Calculating Surface Area: Calculating surface area depends entirely on the shape of the three-dimensional object:
- Cube: Surface Area = 6 × side² (since a cube has six identical square faces)
- Cuboid (Rectangular Prism): Surface Area = 2(length × width + length × height + width × height)
- Sphere: Surface Area = 4 × π × radius²
- Cylinder: Surface Area = 2 × π × radius × height + 2 × π × radius² (lateral surface area + area of two circular bases)
- Cone: Surface Area = π × radius × slant height + π × radius² (lateral surface area + area of circular base)
- Complex Shapes: For complex shapes, the surface area can be calculated by breaking down the object into simpler shapes, calculating the area of each, and summing the results. More advanced techniques using calculus (surface integrals) are sometimes necessary.
Examples of Surface Area in Everyday Life:
- Packaging: The amount of material needed to create a box is determined by its surface area.
- Heat Transfer: The surface area of an object significantly influences how quickly it heats up or cools down.
- Fluid Dynamics: The surface area of an object affects the drag it experiences when moving through a fluid (e.g., air or water).
- Construction: Calculating the surface area of a building's exterior is crucial for estimating the amount of paint, siding, or insulation needed.
- Medical Applications: Understanding surface area is important in various medical contexts, such as calculating drug dosage based on body surface area (BSA) in pediatrics or oncology.
Key Differences Between Surface Area and Area
The fundamental difference lies in the dimensionality:
| Feature | Area | Surface Area |
|---|---|---|
| Dimensionality | Two-dimensional | Three-dimensional (but the measurement itself is two-dimensional) |
| Application | Flat shapes, surfaces of 3D objects | External surfaces of 3D objects |
| Calculation | Varies depending on shape | Varies depending on 3D shape |
| Units | Square units (m², ft², cm², etc.) | Square units (m², ft², cm², etc.) |
Relationship to Volume
While area and surface area are fundamentally different, they are related to volume, the three-dimensional space enclosed within a three-dimensional object. However, there's no direct mathematical relationship between area and volume, or surface area and volume that applies universally across all shapes. The relationship is shape-dependent. For example, two shapes might have the same volume but vastly different surface areas.
Consider a cube and a sphere with the same volume. The sphere will have a smaller surface area than the cube. This difference has significant implications in various contexts, such as minimizing material use in packaging or optimizing heat transfer in engineering applications.
Common Misconceptions
- Confusing Area and Perimeter: Perimeter is the total length of the boundary of a two-dimensional shape. It's a one-dimensional measurement, unlike area, which is two-dimensional.
- Assuming a direct relationship between surface area and volume: There is no constant, universal relationship between surface area and volume for all shapes.
- Not considering the units: Always remember to state the units when measuring area and surface area (e.g., square meters, square feet).
Advanced Applications
The concepts of area and surface area extend far beyond basic geometry. They find applications in:
- Engineering: Designing efficient heat exchangers or optimizing aerodynamic shapes involves careful consideration of surface area.
- Architecture: Calculating material requirements for building construction necessitates precise calculations of surface area.
- Medicine: Determining appropriate drug dosages often involves considering the patient's body surface area.
- Computer Graphics: Rendering realistic 3D images requires accurate surface area calculations for lighting and shading effects.
- Environmental Science: Estimating the surface area of lakes or forests is vital for ecological studies.
Conclusion
Understanding the distinctions between area and surface area is essential for accurately measuring and analyzing two-dimensional and three-dimensional objects. Though both use squared units, the application differs significantly. Area deals with flat shapes and the surfaces of 3D objects, while surface area encompasses the total external area of a three-dimensional object. Mastering these concepts opens doors to solving problems across a multitude of disciplines. Remember to consider the specific shape when calculating either area or surface area and always pay close attention to the units of measurement to ensure accuracy and avoid common misconceptions. By grasping these core principles, you'll develop a more robust understanding of geometric concepts and their real-world applications.
Latest Posts
Latest Posts
-
Is The Square Root Of 36 Rational
Mar 31, 2025
-
Is Condensation A Chemical Or Physical Change
Mar 31, 2025
-
Is Calcium A Metal Nonmetal Or Metalloid
Mar 31, 2025
-
Adjectives That Start With The Letter C
Mar 31, 2025
-
Lcm Of 9 And 12 And 15
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Difference Between Surface Area And Area . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
