Lcm Of 9 And 12 And 15
Juapaving
Mar 31, 2025 · 5 min read
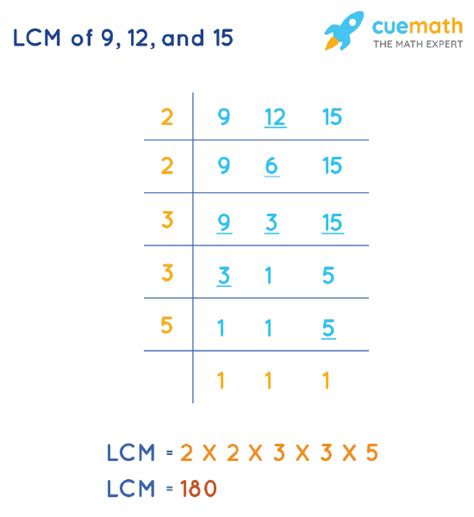
Table of Contents
Finding the Least Common Multiple (LCM) of 9, 12, and 15: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with wide-ranging applications in various fields. This comprehensive guide will walk you through the process of calculating the LCM of 9, 12, and 15, explaining different methods and their underlying principles. We'll delve into the theoretical basis of LCM, explore various techniques for calculating it, and illustrate practical applications to solidify your understanding.
Understanding Least Common Multiples (LCM)
Before we jump into calculating the LCM of 9, 12, and 15, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
Think of it like finding the smallest common denominator when adding or subtracting fractions. The LCM provides the smallest denominator that allows for seamless addition or subtraction.
Methods for Calculating LCM
Several methods exist for calculating the LCM, each offering different advantages depending on the numbers involved and the level of mathematical sophistication desired. We'll explore three common approaches:
1. Listing Multiples Method
This method, ideal for smaller numbers, involves listing the multiples of each number until you find the smallest multiple common to all.
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 135...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225...
By comparing the lists, we observe that the smallest multiple common to 9, 12, and 15 is 180. Therefore, the LCM(9, 12, 15) = 180.
This method is straightforward but becomes cumbersome for larger numbers or a greater number of integers.
2. Prime Factorization Method
This method uses the prime factorization of each number to determine the LCM. Prime factorization involves expressing a number as a product of its prime factors.
-
Prime factorize each number:
- 9 = 3²
- 12 = 2² × 3
- 15 = 3 × 5
-
Identify the highest power of each prime factor:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3² = 9
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers together:
- LCM(9, 12, 15) = 2² × 3² × 5 = 4 × 9 × 5 = 180
This method is more efficient than listing multiples, especially for larger numbers. It provides a systematic approach that avoids the need for extensive listing.
3. Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The formula relating LCM and GCD is:
LCM(a, b) = (a × b) / GCD(a, b)
This can be extended to more than two numbers using iterative application.
-
Find the GCD of 9 and 12 using the Euclidean algorithm:
- 12 = 1 × 9 + 3
- 9 = 3 × 3 + 0
- The GCD(9, 12) = 3
-
Find the LCM of 9 and 12:
- LCM(9, 12) = (9 × 12) / 3 = 36
-
Find the GCD of 36 and 15 using the Euclidean algorithm:
- 36 = 2 × 15 + 6
- 15 = 2 × 6 + 3
- 6 = 2 × 3 + 0
- The GCD(36, 15) = 3
-
Find the LCM of 36 and 15:
- LCM(36, 15) = (36 × 15) / 3 = 180
Therefore, the LCM(9, 12, 15) = 180. While this method involves multiple steps, it showcases the powerful connection between LCM and GCD.
Applications of LCM
The LCM finds extensive applications across various mathematical and real-world scenarios:
- Fractions: Finding the least common denominator when adding or subtracting fractions.
- Scheduling: Determining the time when events with different periodicities will coincide (e.g., buses arriving at a stop).
- Gears and Pulleys: Calculating the speed and synchronization of rotating parts in machinery.
- Music: Determining the frequency of notes and harmonies.
- Modular Arithmetic: Solving congruence equations and other problems in number theory.
Why is finding the LCM important?
Understanding and calculating LCM isn't just an academic exercise; it’s a crucial skill with practical relevance:
-
Efficiency: Finding the LCM allows for efficient problem-solving in various contexts. For instance, in scheduling, determining the LCM helps avoid unnecessary calculations and provides the most efficient solution.
-
Accuracy: In calculations involving fractions, using the LCM as the common denominator ensures accuracy and avoids errors.
-
Foundation for Advanced Concepts: The concept of LCM builds the foundation for understanding more advanced mathematical concepts like modular arithmetic and abstract algebra.
Conclusion: Mastering LCM Calculations
This guide has comprehensively explored different methods for calculating the least common multiple, focusing specifically on finding the LCM of 9, 12, and 15. We’ve demonstrated the listing multiples, prime factorization, and GCD methods, highlighting their advantages and disadvantages. Understanding LCM is vital for tackling various mathematical problems and real-world applications. By mastering these methods, you’ll be well-equipped to efficiently and accurately solve problems involving LCM, enhancing your mathematical proficiency. Remember to choose the method that best suits the numbers involved and your comfort level with different mathematical techniques. The consistent practice of these techniques is crucial to reinforcing your understanding and improving your computational skills.
Latest Posts
Latest Posts
-
What Is The Prime Factorization 81
Apr 01, 2025
-
No Name This Compound According To Iupac Nomenclature Rules Responses
Apr 01, 2025
-
Why Does Heat Not Transfer Through Solids By Convection
Apr 01, 2025
-
Solid Has Definite Shape And Volume
Apr 01, 2025
-
What Animal Lays Eggs Thats Not A Bird
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 9 And 12 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
