What Is The Cubed Root Of 27
Juapaving
Mar 28, 2025 · 5 min read
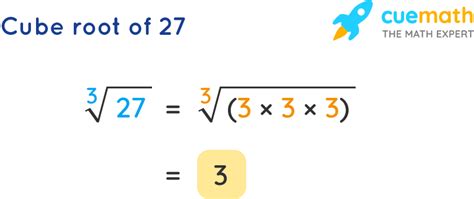
Table of Contents
What is the Cubed Root of 27? A Deep Dive into Cube Roots and Their Applications
The question, "What is the cubed root of 27?" might seem simple at first glance. The answer, 3, is readily apparent to anyone familiar with basic arithmetic. However, delving deeper into the concept of cube roots reveals a rich mathematical landscape with far-reaching applications across various fields. This article will explore the cubed root of 27, its mathematical underpinnings, and its relevance in different contexts, including algebra, geometry, and even real-world problem-solving.
Understanding Cube Roots: A Fundamental Concept
Before we delve into the specifics of the cubed root of 27, let's establish a clear understanding of what a cube root actually is. In mathematics, the cube root of a number is a value that, when multiplied by itself three times (cubed), results in the original number. This is represented symbolically as ∛x, where 'x' is the number whose cube root we are seeking. Therefore, finding the cube root is the inverse operation of cubing a number.
For example:
- The cube root of 8 (∛8) is 2, because 2 x 2 x 2 = 8.
- The cube root of 64 (∛64) is 4, because 4 x 4 x 4 = 64.
- And, as we'll explore in detail, the cube root of 27 (∛27) is 3, because 3 x 3 x 3 = 27.
Calculating the Cubed Root of 27: Methods and Approaches
There are several ways to calculate the cubed root of 27. The simplest method, suitable for smaller numbers like 27, is to identify a number that, when cubed, equals 27. Through basic multiplication, we quickly find that 3 x 3 x 3 = 27. Therefore, the cubed root of 27 is 3.
However, for larger numbers, this trial-and-error approach becomes less efficient. More advanced methods include:
1. Using a Calculator: The Easiest Method
Modern calculators have built-in functions for calculating cube roots. Simply enter 27 and use the cube root function (often denoted as ∛ or x^(1/3)). The calculator will instantly provide the answer: 3. This is the most convenient method for everyday calculations.
2. Prime Factorization: A More Fundamental Approach
Prime factorization is a powerful technique for simplifying calculations involving roots. To find the cube root of 27, we first find its prime factorization:
27 = 3 x 3 x 3 = 3³
Since 27 can be expressed as 3 cubed, its cube root is simply 3. This method is particularly useful for larger numbers where the cube root might not be immediately obvious.
3. Numerical Methods: For More Complex Scenarios
For extremely large numbers or those that don't have whole number cube roots, numerical methods like the Newton-Raphson method can be employed. These iterative methods refine an initial guess until an acceptable level of accuracy is reached. While beyond the scope of a simple calculation like ∛27, these methods are essential in advanced mathematical computing.
The Significance of the Cubed Root of 27: Applications in Different Fields
While the answer "3" might seem straightforward, the concept of cube roots and their calculations have wide-ranging applications across various disciplines:
1. Algebra and Equation Solving
Cube roots are crucial in solving cubic equations – polynomial equations of the third degree. These equations often appear in physics, engineering, and other scientific fields. Understanding cube roots is fundamental to manipulating and solving these equations. For example, an equation like x³ = 27 is solved directly by taking the cube root of both sides, leading to x = 3.
2. Geometry and Volume Calculations
Cube roots are essential in calculating the dimensions of three-dimensional objects. For instance, if you know the volume of a cube, you can find its side length by taking the cube root of the volume. If a cube has a volume of 27 cubic units, its side length is ∛27 = 3 units. This application extends to other geometric shapes where volume calculations involve cubic relationships.
3. Physics and Engineering
Cube roots appear in various physics and engineering formulas. For example, in fluid mechanics, calculations related to flow rates and pipe dimensions often involve cube roots. In structural engineering, determining the stress on a material under pressure might necessitate the use of cube roots in certain formulas.
4. Chemistry and Molecular Structure
In chemistry, cube roots can be relevant in calculations involving molarity and concentration. Understanding how cube roots relate to volume and quantity is essential for precise chemical calculations.
5. Data Analysis and Statistics
While less direct, cube roots can appear in statistical analyses, particularly when dealing with data transformations or specific statistical distributions.
Beyond the Simple Answer: Exploring Complex Cube Roots
While the cube root of 27 is a straightforward positive integer (3), the concept of cube roots extends to complex numbers. For negative numbers, the cube root will also be a real number, but it will be negative. For example, ∛-27 = -3 because (-3) x (-3) x (-3) = -27.
The concept becomes even more nuanced when considering complex numbers, where cube roots can have multiple solutions, including complex numbers with both real and imaginary parts. This delves into the realm of complex analysis, a more advanced area of mathematics.
Practical Applications and Problem-Solving
Let's consider a real-world example to illustrate the application of cube roots:
Problem: A water tank is in the shape of a cube. Its volume is measured to be 125 cubic meters. What is the length of one side of the tank?
Solution: Since the tank is a cube, the volume (V) is given by V = side³ (where 'side' is the length of one side). We know that V = 125 cubic meters. To find the side length, we take the cube root of the volume:
Side = ∛125 = 5 meters
Therefore, the length of one side of the water tank is 5 meters.
Conclusion: The Ubiquity of Cube Roots
The seemingly simple question of "What is the cubed root of 27?" opens a gateway to a vast and intricate mathematical landscape. While the answer, 3, is readily available, the underlying concept of cube roots and their applications extend far beyond this basic calculation. From solving algebraic equations to calculating volumes in geometry and tackling complex problems in physics and engineering, cube roots play a significant role in various fields, highlighting their fundamental importance in mathematics and its real-world applications. Understanding cube roots, therefore, is not just about memorizing a simple answer but about grasping a powerful mathematical tool with wide-reaching implications.
Latest Posts
Latest Posts
-
What Is The Prime Factorization Of 216
Mar 31, 2025
-
Suez Canal Connects Which Two Bodies Of Water
Mar 31, 2025
-
How Many Vertices Do A Square Have
Mar 31, 2025
-
Lcm Of 3 9 And 12
Mar 31, 2025
-
How Many Feet In 95 Inches
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Cubed Root Of 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
