What Is The Prime Factorization Of 216
Juapaving
Mar 31, 2025 · 5 min read
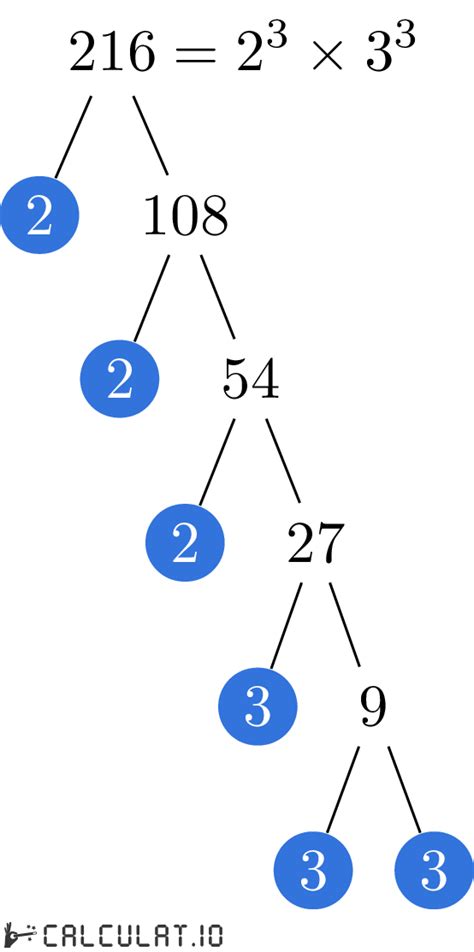
Table of Contents
What is the Prime Factorization of 216? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What is the prime factorization of 216?" opens a door to a fascinating world of number theory. While the answer itself might be quickly obtained with a calculator or online tool, understanding the process of finding the prime factorization, and the underlying concepts of prime numbers and factorization, is crucial for anyone interested in mathematics, computer science, or cryptography. This article will not only provide the answer but also delve deep into the methodology, explaining the concepts involved in a clear and accessible way, incorporating relevant SEO keywords throughout.
Understanding Prime Numbers
Before we tackle the prime factorization of 216, let's establish a strong foundation by understanding what prime numbers are. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. This sequence extends infinitely, a fact proven by Euclid over two thousand years ago. Prime numbers are the fundamental building blocks of all other integers.
Identifying Prime Numbers: A Quick Guide
Identifying whether a number is prime can be surprisingly challenging for larger numbers. However, for smaller numbers, a few simple checks can help:
- Divisibility by 2: If the number is even (ends in 0, 2, 4, 6, or 8), it's divisible by 2 and therefore not prime (except for 2 itself).
- Divisibility by 3: If the sum of the digits is divisible by 3, the number is divisible by 3.
- Divisibility by 5: If the number ends in 0 or 5, it's divisible by 5.
- Divisibility by 7: There's no simple rule for 7, but you can test for divisibility.
For larger numbers, more sophisticated methods, like the Sieve of Eratosthenes, are employed. These algorithms efficiently identify prime numbers within a given range.
What is Factorization?
Factorization is the process of breaking down a composite number (a number that is not prime) into its prime number components. Every composite number can be uniquely expressed as a product of prime numbers. This unique representation is called the prime factorization of the number. This principle is fundamental to many areas of mathematics and is the cornerstone of various cryptographic systems.
The Fundamental Theorem of Arithmetic
The uniqueness of prime factorization is guaranteed by the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be represented as a product of prime numbers in a unique way, up to the order of the factors. This means that no matter how you factorize a number, you'll always end up with the same set of prime factors. This seemingly simple statement has profound implications in various mathematical fields.
Finding the Prime Factorization of 216: A Step-by-Step Approach
Now, let's find the prime factorization of 216 using a systematic approach:
-
Start with the smallest prime number: We begin by checking divisibility by 2. Since 216 is an even number, it's divisible by 2. 216 = 2 × 108
-
Continue with the smallest prime factor: 108 is also even, so we divide by 2 again: 108 = 2 × 54
-
Repeat the process: 54 is also even: 54 = 2 × 27
-
Move to the next prime number: 27 is not divisible by 2, but it is divisible by 3: 27 = 3 × 9
-
Continue factoring: 9 is also divisible by 3: 9 = 3 × 3
-
We've reached prime factors: We've now expressed 216 as a product of prime numbers: 2 × 2 × 2 × 3 × 3 × 3.
-
Expressing in exponential form: To write the prime factorization concisely, we use exponents: 2<sup>3</sup> × 3<sup>3</sup>.
Therefore, the prime factorization of 216 is 2<sup>3</sup> × 3<sup>3</sup>. This means 216 is composed of three factors of 2 and three factors of 3.
Applications of Prime Factorization
The concept of prime factorization, while seemingly abstract, has numerous real-world applications:
-
Cryptography: Many modern encryption methods, such as RSA, rely heavily on the difficulty of factoring very large numbers into their prime components. The security of these systems hinges on the computational intractability of this problem for sufficiently large numbers.
-
Computer Science: Prime factorization plays a significant role in algorithms used in computer science, particularly in areas like hashing, data structures, and network security.
-
Number Theory: Prime factorization is a fundamental concept in number theory, forming the basis for various theorems and proofs.
-
Mathematics Education: Understanding prime factorization helps develop crucial mathematical skills, including logical reasoning, problem-solving, and pattern recognition.
Beyond 216: Exploring Prime Factorization of Other Numbers
The process outlined above can be applied to find the prime factorization of any composite number. Let's consider a few more examples:
Example 1: Prime Factorization of 360
- 360 = 2 × 180
- 180 = 2 × 90
- 90 = 2 × 45
- 45 = 3 × 15
- 15 = 3 × 5
Therefore, the prime factorization of 360 is 2<sup>3</sup> × 3<sup>2</sup> × 5.
Example 2: Prime Factorization of 1000
- 1000 = 2 × 500
- 500 = 2 × 250
- 250 = 2 × 125
- 125 = 5 × 25
- 25 = 5 × 5
Therefore, the prime factorization of 1000 is 2<sup>3</sup> × 5<sup>3</sup>.
Conclusion: The Significance of Prime Factorization
The prime factorization of 216, and the broader concept of prime factorization itself, is far more than a simple mathematical exercise. It's a fundamental building block in various fields, showcasing the power and elegance of mathematical principles. Understanding the process and the underlying concepts not only enhances mathematical literacy but also provides valuable insights into the foundations of computer science, cryptography, and other related disciplines. The seemingly simple question, "What is the prime factorization of 216?", thus reveals a rich and intricate tapestry of mathematical ideas. From the basic definition of prime numbers to the advanced applications in modern cryptography, the journey into prime factorization opens up a world of fascinating exploration.
Latest Posts
Latest Posts
-
Are There Centrioles In Plant Cells
Apr 02, 2025
-
Common Factors Of 35 And 50
Apr 02, 2025
-
What Is The Difference Between Ac And Dc Motors
Apr 02, 2025
-
Subject And Predicate Exercises With Answers
Apr 02, 2025
-
Greater Than Less Than Decimal Calculator
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization Of 216 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
