How Many Vertices Do A Square Have
Juapaving
Mar 31, 2025 · 5 min read
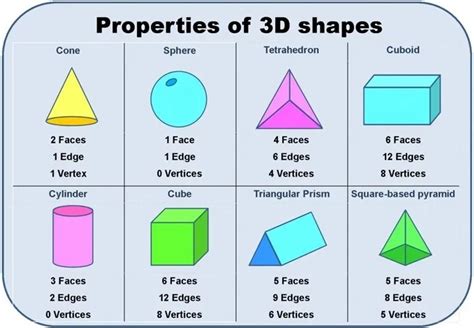
Table of Contents
How Many Vertices Does a Square Have? A Deep Dive into Geometry
The seemingly simple question, "How many vertices does a square have?" opens a door to a fascinating exploration of geometry, its fundamental concepts, and its broader applications. While the immediate answer is four, delving deeper reveals a wealth of interconnected ideas that are crucial to understanding more complex geometric structures and their practical uses. This article will not only answer the question definitively but also explore the underlying principles, related concepts, and the significance of vertices in various fields.
Understanding Basic Geometric Terminology
Before we definitively answer how many vertices a square has, let's solidify our understanding of key terms. This foundational knowledge is crucial for comprehending more complex geometric concepts.
What is a Vertex?
A vertex (plural: vertices) is a point where two or more lines or edges meet. Think of it as a corner. In two-dimensional shapes, vertices are the points that define the shape's boundaries. In three-dimensional shapes, vertices are the points where edges intersect.
What is a Square?
A square is a two-dimensional, four-sided polygon (a shape with straight sides) with the following defining characteristics:
- Four equal sides: All sides are of the same length.
- Four right angles: Each interior angle measures 90 degrees.
- Opposite sides are parallel: This property ensures the stability and regularity of the square.
Now, with these definitions clearly established, we can confidently answer the central question.
The Definitive Answer: A Square Has Four Vertices
A square, by definition, possesses four vertices. These vertices are the four corners of the square, where its sides meet. Each vertex represents a point of intersection, marking the boundaries and defining the shape's overall structure.
Beyond the Simple Answer: Exploring Related Concepts
Understanding the number of vertices in a square is just the beginning. This simple understanding opens doors to exploring numerous related concepts in geometry and mathematics.
Polygons and Their Vertices
A polygon is a closed two-dimensional figure formed by joining a sequence of straight line segments. The number of vertices a polygon has directly corresponds to the number of sides it possesses. For example:
- Triangle: 3 sides, 3 vertices
- Quadrilateral: 4 sides, 4 vertices (Squares, rectangles, rhombuses, and trapezoids are all quadrilaterals)
- Pentagon: 5 sides, 5 vertices
- Hexagon: 6 sides, 6 vertices
- And so on...
The relationship between the number of sides and vertices in polygons is fundamental to understanding their properties and classifications.
Angles and Their Relationship to Vertices
Each vertex in a polygon is associated with an interior angle. The sum of the interior angles of a polygon is dependent on the number of sides (and therefore vertices) it has. For a square, the sum of its interior angles is 360 degrees (90 degrees per vertex). This relationship extends to all polygons, providing a way to calculate interior angle sums based solely on the number of vertices.
Coordinate Geometry and Vertices
In coordinate geometry, vertices are represented by ordered pairs (x, y) on a Cartesian plane. These coordinates precisely locate each vertex, allowing for the mathematical description and manipulation of the square. This precise location is crucial for calculations involving area, perimeter, and transformations (rotations, translations, reflections).
Applications in Computer Graphics and Design
The concept of vertices is central to computer graphics and computer-aided design (CAD). Shapes, objects, and scenes are represented as collections of vertices connected by edges, forming polygons that approximate curved surfaces. The manipulation and rendering of these shapes rely heavily on the precise location and properties of their vertices. Consider 3D modeling software; the intricate shapes and forms we see are all built upon the foundation of connecting vertices.
Vertices in Network Theory
Vertices also play a critical role in graph theory, a branch of mathematics used to model networks. In a network graph, vertices represent nodes (e.g., computers in a network, cities in a transportation system), and edges represent connections between these nodes. Analyzing the connectivity and properties of these networks is crucial in various fields, including social network analysis, logistics, and telecommunications. Understanding the structure defined by the vertices and edges allows for efficient routing, resource allocation, and network optimization.
Extending the Concept: Three-Dimensional Shapes and Beyond
While our focus has been on two-dimensional squares, the concept of vertices extends to three-dimensional shapes and beyond.
Three-Dimensional Shapes and Their Vertices
Consider a cube, a three-dimensional analogue of a square. A cube has eight vertices, each representing the point where three edges meet. This principle extends to other three-dimensional shapes like pyramids, prisms, and more complex polyhedra. The number of vertices varies depending on the shape's structure, but they always represent points of intersection.
The Importance of Vertices: A Summary
The seemingly simple question of how many vertices a square possesses unlocks a gateway to a deeper understanding of geometric concepts. From the fundamental relationship between sides and vertices in polygons to the applications in computer graphics, network theory, and beyond, vertices serve as essential building blocks for complex systems and representations. Their precise location and properties are crucial in various calculations, analyses, and applications. The seemingly simple answer—"four"—lays the foundation for a rich and multifaceted exploration of the mathematical world.
Further Exploration: Challenging Your Understanding
To solidify your understanding, consider these thought-provoking questions:
- How does the number of vertices in a polygon affect its area and perimeter calculations?
- How can you use coordinate geometry to determine if four given points form a square?
- Can you identify real-world examples where understanding vertices is crucial? (Consider architecture, engineering, or game design)
- Research and describe the Euler's formula for polyhedra, which relates the number of vertices, edges, and faces.
By exploring these questions and delving deeper into the concepts discussed, you'll gain a more profound appreciation for the significance of vertices in mathematics and its applications across diverse fields. The seemingly simple question of how many vertices a square has serves as an excellent starting point for a rich and rewarding exploration of geometry and its importance in the world around us.
Latest Posts
Latest Posts
-
Common Factors Of 35 And 50
Apr 02, 2025
-
What Is The Difference Between Ac And Dc Motors
Apr 02, 2025
-
Subject And Predicate Exercises With Answers
Apr 02, 2025
-
Greater Than Less Than Decimal Calculator
Apr 02, 2025
-
How Many Times Does 4 Go Into 72
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How Many Vertices Do A Square Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
