Lcm Of 3 9 And 12
Juapaving
Mar 31, 2025 · 5 min read
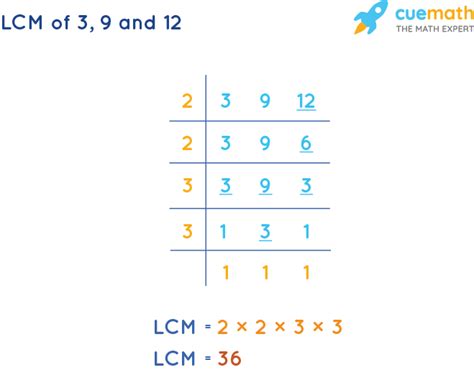
Table of Contents
Finding the LCM of 3, 9, and 12: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and beyond. This article delves deep into calculating the LCM of 3, 9, and 12, exploring multiple methods and highlighting the underlying mathematical principles. We'll also discuss the broader context of LCMs and their practical uses.
Understanding Least Common Multiple (LCM)
Before we tackle the specific LCM of 3, 9, and 12, let's establish a firm understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The smallest of these common multiples is 6; therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM
Several methods can be employed to find the LCM of a set of numbers. We will explore the most common and effective approaches:
1. Listing Multiples Method
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all.
Let's apply this to our numbers, 3, 9, and 12:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 36...
- Multiples of 9: 9, 18, 27, 36, 45...
- Multiples of 12: 12, 24, 36, 48...
By comparing the lists, we observe that the smallest common multiple is 36. Therefore, the LCM(3, 9, 12) = 36. This method works well for small numbers but becomes increasingly cumbersome as the numbers get larger.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Let's break down 3, 9, and 12 into their prime factors:
- 3 = 3¹ (3 is a prime number)
- 9 = 3² (9 = 3 x 3)
- 12 = 2² x 3¹ (12 = 2 x 2 x 3)
Now, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3² = 9
To find the LCM, we multiply these highest powers together:
LCM(3, 9, 12) = 2² x 3² = 4 x 9 = 36
This method is more systematic and efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related. We can use the GCD to calculate the LCM using the following formula:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
First, we need to find the GCD of 3, 9, and 12. The GCD is the largest number that divides all three numbers without leaving a remainder. In this case, the GCD(3, 9, 12) = 3.
Now, we can apply the formula:
LCM(3, 9, 12) = (3 x 9 x 12) / 3 = 108 / 3 = 36
This method requires calculating the GCD first, but it provides an alternative approach, particularly useful when dealing with larger numbers where finding the prime factorization might be more challenging.
Applications of LCM
The concept of the least common multiple finds applications in various areas of mathematics and beyond:
- Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators.
- Scheduling Problems: Determining when events will occur simultaneously, such as buses arriving at a bus stop or machines completing cycles, often requires calculating the LCM.
- Modular Arithmetic: LCM plays a significant role in solving problems related to congruences and modular arithmetic.
- Music Theory: LCM helps in determining the least common period of two or more musical notes or rhythms.
- Engineering and Computer Science: LCM is utilized in various computational tasks and process synchronization.
Further Exploration: LCM of More Than Three Numbers
The methods discussed above can be extended to find the LCM of more than three numbers. The prime factorization method remains particularly effective. For example, to find the LCM of 4, 6, 8, and 12:
-
Prime Factorization:
- 4 = 2²
- 6 = 2 x 3
- 8 = 2³
- 12 = 2² x 3
-
Identify Highest Powers:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
-
Calculate LCM: LCM(4, 6, 8, 12) = 2³ x 3 = 8 x 3 = 24
Conclusion
Finding the LCM, whether it's for the simple case of 3, 9, and 12 or for more complex sets of numbers, is a crucial skill in mathematics. Understanding the different methods—listing multiples, prime factorization, and the GCD method—allows you to choose the most efficient approach based on the numbers involved. The concept of LCM extends far beyond simple mathematical exercises, finding practical application in various fields, highlighting its importance in both theoretical and applied mathematics. Mastering LCM calculation enhances your mathematical proficiency and opens doors to solving a wider range of problems. Remember that the choice of method often depends on the size and complexity of the numbers you are working with. For smaller numbers, listing multiples is perfectly acceptable. However, for larger numbers, the prime factorization method proves far more efficient and less prone to error. Understanding both methods provides a well-rounded skill set for tackling LCM problems effectively.
Latest Posts
Latest Posts
-
What Is The Difference Between Ac And Dc Motors
Apr 02, 2025
-
Subject And Predicate Exercises With Answers
Apr 02, 2025
-
Greater Than Less Than Decimal Calculator
Apr 02, 2025
-
How Many Times Does 4 Go Into 72
Apr 02, 2025
-
How Do You Factorize An Equation
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 9 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
