What Is The Binary Equivalent Of Decimal 15
Juapaving
Mar 24, 2025 · 6 min read
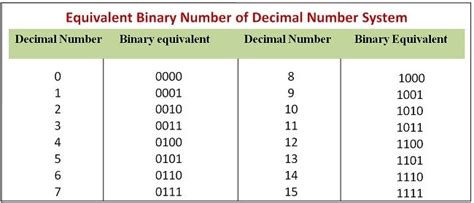
Table of Contents
- What Is The Binary Equivalent Of Decimal 15
- Table of Contents
- What is the Binary Equivalent of Decimal 15? A Deep Dive into Number Systems
- Understanding Number Systems
- The Decimal System (Base-10)
- The Binary System (Base-2)
- Finding the Binary Equivalent of Decimal 15
- Method 1: Repeated Division by 2
- Method 2: Place Value Method
- Other Number Systems and Their Conversions
- Octal (Base-8)
- Hexadecimal (Base-16)
- Practical Applications of Binary and Other Number Systems
- Computer Architecture
- Data Storage and Representation
- Network Communication
- Programming and Software Development
- Error Detection and Correction
- Conclusion: The Significance of Understanding Binary
- Latest Posts
- Latest Posts
- Related Post
What is the Binary Equivalent of Decimal 15? A Deep Dive into Number Systems
The seemingly simple question, "What is the binary equivalent of decimal 15?" opens a door to a fascinating world of number systems, crucial for understanding how computers and digital devices function. This article will not only answer that question but will delve deep into the concepts behind binary, decimal, and other number systems, exploring their conversions and practical applications.
Understanding Number Systems
Before diving into the specifics of decimal 15's binary equivalent, let's establish a firm foundation in the concept of number systems. A number system is essentially a way of representing numbers using a set of symbols and rules. Different number systems utilize different bases (or radices), which determine the number of unique digits available.
The Decimal System (Base-10)
The decimal system, the one we use every day, is a base-10 system. This means it uses ten unique digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Each position in a decimal number represents a power of 10. For example, the number 1234 can be broken down as:
- 1 x 10³ (1000)
- 2 x 10² (200)
- 3 x 10¹ (30)
- 4 x 10⁰ (4)
The sum of these values (1000 + 200 + 30 + 4) gives us 1234.
The Binary System (Base-2)
The binary system, the language of computers, is a base-2 system. It only uses two digits: 0 and 1. Each position in a binary number represents a power of 2. This simplicity is what makes it ideal for electronic circuits, where the presence or absence of an electrical signal can be easily represented by 1 and 0 respectively.
Let's consider the binary number 1011. We can break it down as:
- 1 x 2³ (8)
- 0 x 2² (0)
- 1 x 2¹ (2)
- 1 x 2⁰ (1)
Adding these values (8 + 0 + 2 + 1) gives us 11 in decimal.
Finding the Binary Equivalent of Decimal 15
Now, let's address the core question: what is the binary equivalent of decimal 15? We can find this using several methods.
Method 1: Repeated Division by 2
This is a systematic approach. We repeatedly divide the decimal number by 2 and record the remainders. The remainders, read in reverse order, form the binary equivalent.
- 15 ÷ 2 = 7 remainder 1
- 7 ÷ 2 = 3 remainder 1
- 3 ÷ 2 = 1 remainder 1
- 1 ÷ 2 = 0 remainder 1
Reading the remainders from bottom to top, we get 1111. Therefore, the binary equivalent of decimal 15 is 1111.
Method 2: Place Value Method
This method involves finding the largest power of 2 that is less than or equal to the decimal number and then subtracting it. We repeat this process until we reach 0.
- The largest power of 2 less than or equal to 15 is 2³ (8). 15 - 8 = 7.
- The largest power of 2 less than or equal to 7 is 2² (4). 7 - 4 = 3.
- The largest power of 2 less than or equal to 3 is 2¹ (2). 3 - 2 = 1.
- The largest power of 2 less than or equal to 1 is 2⁰ (1). 1 - 1 = 0.
This gives us 2³ + 2² + 2¹ + 2⁰ = 8 + 4 + 2 + 1 = 15. Representing this in binary, we have 1 (2³) + 1 (2²) + 1 (2¹) + 1 (2⁰) = 1111.
Other Number Systems and Their Conversions
While binary and decimal are the most commonly used, other number systems exist, each with its own base and applications.
Octal (Base-8)
The octal system uses eight digits (0-7). Each position represents a power of 8. Octal is sometimes used as a shorthand for representing binary numbers, as each octal digit can be represented by three binary digits.
Hexadecimal (Base-16)
The hexadecimal system uses sixteen digits (0-9 and A-F, where A represents 10, B represents 11, and so on). Each position represents a power of 16. Hexadecimal is frequently used in computer programming and data representation because it provides a compact way to represent binary data.
Converting between these systems often involves similar methods to those used for binary-decimal conversion. For instance, you can convert decimal to hexadecimal by repeatedly dividing by 16 and recording the remainders, similar to the method used for binary conversion.
Practical Applications of Binary and Other Number Systems
Understanding different number systems is not just an academic exercise; it's crucial for comprehending how computers and digital technology function.
Computer Architecture
At the heart of every computer lies its ability to process and store information using binary. Transistors, the fundamental building blocks of computer circuits, can represent either a high voltage (1) or a low voltage (0). This binary representation allows computers to perform complex operations by manipulating sequences of 0s and 1s.
Data Storage and Representation
Files, images, videos, and other digital data are all stored and represented in binary format. Each bit (binary digit) contributes to the overall information encoded. This binary data is often grouped into bytes (8 bits), words (16, 32, or 64 bits), and other units depending on the system's architecture.
Network Communication
Data transmitted over networks, including the internet, uses binary encoding. Protocols define how data is structured and formatted for transmission, relying heavily on binary representation for efficient and reliable communication.
Programming and Software Development
Programmers frequently interact with binary concepts, particularly when working at lower levels of the system, such as dealing with memory addresses, bitwise operations, or low-level network programming.
Error Detection and Correction
Binary codes are also used in error detection and correction techniques. By adding extra bits to the data (checksums or parity bits), it's possible to detect and correct errors that may occur during transmission or storage.
Conclusion: The Significance of Understanding Binary
The simple question of finding the binary equivalent of decimal 15 has led us on a journey through the world of number systems. We've explored the core principles of different bases, mastered conversion techniques, and understood the vital role that binary plays in computing and digital technology. This knowledge is fundamental to anyone seeking a deeper understanding of how the digital world works, whether you're a computer scientist, programmer, or simply a curious individual fascinated by the inner workings of technology. Mastering binary and other number systems empowers you to appreciate the elegance and power behind the seemingly simple 0s and 1s that drive the digital revolution. As you continue your exploration of computing and technology, remember that this foundational understanding of number systems will serve as a robust base for further learning and advancement.
Latest Posts
Latest Posts
-
Is Melting Butter Physical Or Chemical Change
Mar 29, 2025
-
What Is The Electron Configuration Of Rb
Mar 29, 2025
-
What Is The Least Common Multiple Of 15 And 24
Mar 29, 2025
-
Where In The Cell Does The Krebs Cycle Take Place
Mar 29, 2025
-
The Slope Of A Line On A Distance Time Graph Is
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is The Binary Equivalent Of Decimal 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
